题目内容
已知函数
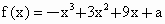 .
.
(1)
求f(x)的单调递减区间;(2)
若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.(2005
·北京)
答案:略
解析:
提示:
解析:
|
(1)∵ ∴ 函数f(x)的单调递减区间为(-∞,-1),(3,+∞).(2)∵f( -2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a ∴f(2)>f(-2). 于是有22+a=20,∴a=-2. ∴ ∵ 在(-1,3)上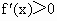 ,∴f(x)在[-1,2]上单调递增. ,∴f(x)在[-1,2]上单调递增.
又由于 f(x)在[-2,-1]上单调递减,∴f(2) 和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值.∴f( -1)=1+3-9-2=-7.即函数 f(x)在区间[-2,2]上的最小值为-7. |
提示:
|
解析:本题主要考查利用导数求函数的单调区间及最值的方法.第 (1)小题应先求 |

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
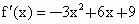 .令
.令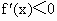 ,解得x<-1或x>3,
,解得x<-1或x>3,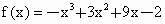
 .
. 的单调区间;
的单调区间; ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围. ,
,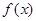 的单调递减区间;
的单调递减区间; 时,求函数
时,求函数 .
. .
. 的单调区间;
的单调区间; 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由; 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解. ,
,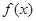 的最小值;
的最小值; 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.