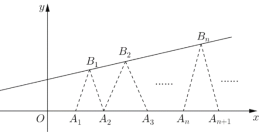
题目内容
【题目】有![]() 个人聚会,已知:
个人聚会,已知:
(1)每个人至少同其中![]() 个人互相认识;
个人互相认识;
(2)对于其中任意![]() 个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这
个人,或者其中有2人相识,或者余下的人中有2人相识,证明:这![]() 个人中必有3人两两相识.
个人中必有3人两两相识.
【答案】见解析
【解析】
假设这![]() 个人中无3人彼此相识.
个人中无3人彼此相识.
设![]() ,
,![]() 是这
是这![]() 个人中相识的2人,由反证假设可推出余下的
个人中相识的2人,由反证假设可推出余下的![]() 个人中,无1人与
个人中,无1人与![]() ,
,![]() 皆相识.因此,至少有
皆相识.因此,至少有![]() 个不同的人,其中每个人或同
个不同的人,其中每个人或同![]() 相识,或同
相识,或同![]() 相识.
相识.
当![]() 为偶数时,由上述讨论可知,这
为偶数时,由上述讨论可知,这![]() 个人中恰有一半人与
个人中恰有一半人与![]() 相识,而另一半人则与
相识,而另一半人则与![]() 相识.于是,由题设可推出在某一半人中必含2个相识的人.这与反证假设矛盾.
相识.于是,由题设可推出在某一半人中必含2个相识的人.这与反证假设矛盾.
当![]() 为奇数时,
为奇数时,![]() .若这几个人中每人与
.若这几个人中每人与![]() 或
或![]() 相识,则与上述讨论类似,可推出矛盾.
相识,则与上述讨论类似,可推出矛盾.
不然,存在![]() ,他同
,他同![]() ,
,![]() 皆不相识,于是,
皆不相识,于是,![]() 个人中除
个人中除![]() 之外的
之外的![]() 个人中必有一半与
个人中必有一半与![]() 相识,另一半与
相识,另一半与![]() 相识.所有
相识.所有![]() 相识的人互不相识,所有与
相识的人互不相识,所有与![]() 相识的人也互不相识.
相识的人也互不相识.
假设有![]() 个人同
个人同![]() ,
,![]() 皆相识,
皆相识,![]() 个人同
个人同![]() ,
,![]() 皆相识,不难由题设推出
皆相识,不难由题设推出![]() ,并且这
,并且这![]() 个人构成与
个人构成与![]() 相识的人的全部.因而,
相识的人的全部.因而,![]() .不妨设
.不妨设![]() ,由
,由![]() 可知
可知![]() .
.
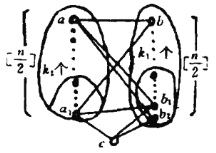
设![]() 同
同![]() ,
,![]() 皆相识,
皆相识,![]() 与
与![]() 同
同![]() ,
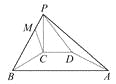
,![]() 皆相识(如图),由于
皆相识(如图),由于![]() 个人中同
个人中同![]() 相识的人至少为
相识的人至少为![]() 个,他们中除
个,他们中除![]() 外同
外同![]() 都相识,故
都相识,故![]() 必与
必与![]() ,
,![]() 之一相识.不妨设
之一相识.不妨设![]() 与
与![]() 相识,则
相识,则![]() ,
,![]() 与
与![]() 是彼此相识的人,此与反证假设相矛盾.因此命题为真.
是彼此相识的人,此与反证假设相矛盾.因此命题为真.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目