题目内容
已知c>0,设命题P:函数y=-c-x为减函数;命题q:当x∈[ ,3]时,函数f(x)=x+
,3]时,函数f(x)=x+
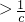 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
解:∵c>0,y=-c-x为减函数,∴0<c<1,
∵函数y=x+ 在[
在[ ,1]递减,在[1,3]上递减,
,1]递减,在[1,3]上递减,
∴在[ ,3]上的值域是:y∈[2,
,3]上的值域是:y∈[2, ],
],
∵y> 恒成立,∴
恒成立,∴ <2?c>
<2?c>
∵p或q为真命题,p且q为假命题,∴P、q命题一真一假

∵c>0,∴c≥1或0<c≤
综上 c∈{c|0<c≤ 或c≥1}
或c≥1}
分析:利用复合指数函数的单调性求命题P为真的c的范围;先求f(x)的最小值,分析函数f(x)=x+
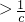 恒成立的条件,然后解出命题q为真命题的c的范围;
恒成立的条件,然后解出命题q为真命题的c的范围;
根据p或q为真命题,p且q为假命题,则P、q命题一真一假,求解.
点评:本题考查复合命题的真假判定,要注意用数学结合进行数集的交、并、补运算.要注意端点能否取到,这是此类题的易错点.
∵函数y=x+
 在[
在[ ,1]递减,在[1,3]上递减,
,1]递减,在[1,3]上递减,∴在[
 ,3]上的值域是:y∈[2,
,3]上的值域是:y∈[2, ],
],∵y>
 恒成立,∴
恒成立,∴ <2?c>
<2?c>
∵p或q为真命题,p且q为假命题,∴P、q命题一真一假

∵c>0,∴c≥1或0<c≤

综上 c∈{c|0<c≤
 或c≥1}
或c≥1}分析:利用复合指数函数的单调性求命题P为真的c的范围;先求f(x)的最小值,分析函数f(x)=x+

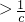 恒成立的条件,然后解出命题q为真命题的c的范围;
恒成立的条件,然后解出命题q为真命题的c的范围;根据p或q为真命题,p且q为假命题,则P、q命题一真一假,求解.
点评:本题考查复合命题的真假判定,要注意用数学结合进行数集的交、并、补运算.要注意端点能否取到,这是此类题的易错点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目