题目内容
(坐标系与参数方程选做题)在极坐标系中,从极点O作直线与另一直线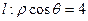 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使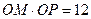 .设R为
.设R为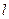 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .
1
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
(坐标系与参数方程选做题)在极坐标系中,从极点O作直线与另一直线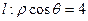 相交于点M,在OM上取一点P,使
相交于点M,在OM上取一点P,使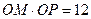 .设R为
.设R为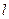 上任意一点,则RP的最小值 .
上任意一点,则RP的最小值 .
1
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案