题目内容
已知 ,命题
,命题 :对任意
:对任意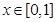 ,不等式
,不等式 恒成立;命题
恒成立;命题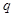 :存在
:存在 ,使得
,使得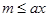 成立
成立
(Ⅰ)若 为真命题,求
为真命题,求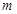 的取值范围;
的取值范围;
(Ⅱ)当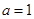 ,若
,若 且
且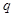 为假,
为假, 或
或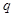 为真,求
为真,求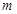 的取值范围。
的取值范围。
(Ⅲ)若 且
且 是
是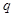 的充分不必要条件,求
的充分不必要条件,求 的取值范围。
的取值范围。
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ)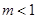 或
或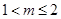 ;(Ⅲ)
;(Ⅲ) 。
。
【解析】
试题分析:(Ⅰ)∵对任意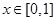 ,不等式
,不等式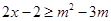 恒成立
恒成立
∴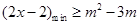 .....................1分
.....................1分
即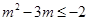 .........................2分
.........................2分
解得 ..............................3分
..............................3分
即 为真命题时,
为真命题时, 的取值范围是
的取值范围是 .......................4分
.......................4分
(Ⅱ)∵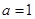 ,且存在
,且存在 ,使得
,使得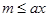 成立
成立
∴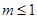
即命题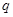 满足
满足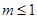 ................5分
................5分
∵ 且
且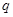 为假,
为假, 或
或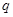 为真
为真
∴ 、
、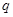 一真一假...........................6分
一真一假...........................6分
当 真
真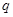 假时,则
假时,则
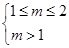 ,即
,即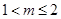 .......................7分
.......................7分
当 假
假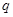 真时,则
真时,则
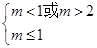 ,即
,即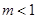 ......................8分
......................8分
综上所述,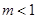 或
或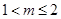 (也可写为
(也可写为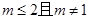 )......................9分
)......................9分
(Ⅲ)∵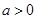 存在
存在 ,使得
,使得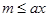 成立
成立
∴命题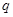 满足
满足 ...........................10分
...........................10分
∵ 是
是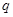 的充分不必要条件
的充分不必要条件
∴ .......................12分
.......................12分
考点:命题真假的判断;含有逻辑连接词的命题;有关恒成立的问题。
点评:若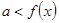 恒成立,只需
恒成立,只需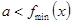 ;若
;若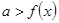 恒成立,则只需
恒成立,则只需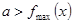 。
。

练习册系列答案
相关题目
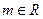 ,命题
,命题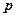 :对任意
:对任意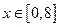 ,不等式
,不等式 恒成立;命题
恒成立;命题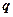 :存在
:存在 ,使不等式
,使不等式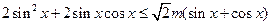 成立.
成立.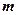 的取值范围;
的取值范围;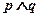 为假,
为假, 为真,求
为真,求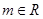 ,命题
,命题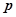 :对任意
:对任意 ,不等式
,不等式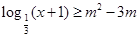 恒成立;命题
恒成立;命题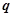 :存在
:存在 ,使不等式
,使不等式 成立.
成立.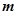 的取值范围;
的取值范围;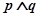 为假,
为假,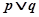 为真,求
为真,求