题目内容
请写出一个整系数多项式f（x），使得| 2 |
| 3 | 3 |
分析：由(
+
)2=2+
+2
，设f（x）=（x2-2）3=((
+
) 2-2)3，变形整理可得答案．
| 2 |
| 3 | 3 |
| 3 | 9 |
| 2 |
| 3 | 3 |
| 2 |
| 3 | 3 |
解答：解：由f（x）=（x2-2）3=((
+
) 2-2)3，
得整系数多项式f（x）=x6-6x4+12x2-8，
∴f（
+
）=(
+
) 6-6(
+
) 4+12(
+
) 2-8
| 2 |
| 3 | 3 |
得整系数多项式f（x）=x6-6x4+12x2-8，
∴f（
| 2 |
| 3 | 3 |
| 2 |
| 3 | 3 |
| 2 |
| 3 | 3 |
| 2 |
| 3 | 3 |
点评：本题考查根式的化简运算，解题时要注意公式的灵活运用．
练习册系列答案
相关题目
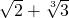是其一个根．
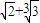是其一个根．