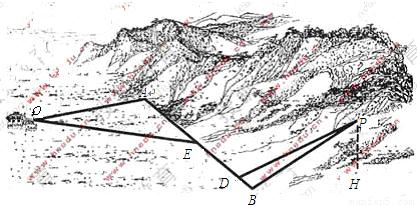
题目内容
如图,某地为了开发旅游资源,欲修建一条连接风景点P和居民区O的公路,点P所在的山坡面与山脚所在水平面α所成的二面角为θ(0°<θ<90°),且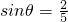 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),
万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),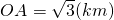 .
.
(I)在AB上求一点D,使沿折线PDAO修建公路的总造价最小;
(II)对于(I)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小.
(III)在AB上是否存在两个不同的点D',E',使沿折线PD'E'O修建公路的总造价小于(II)中得到的最小总造价,证明你的结论、
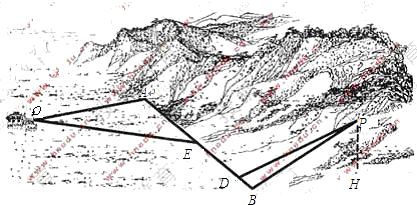
 解:(I)如图,PH⊥α,HB?α,PB⊥AB,
解:(I)如图,PH⊥α,HB?α,PB⊥AB,由三垂线定理逆定理知,AB⊥HB,
所以∠PBH是山坡与α所成二面角的平面角,
则∠PBH=θ,
 .
.设BD=x(km),0≤x≤1.5,
则
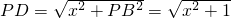 ∈[1,2].
∈[1,2].记总造价为f1(x)万元,
据题设有
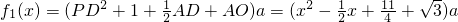 =
=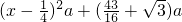
当
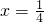 ,即
,即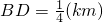 时,总造价f1(x)最小.
时,总造价f1(x)最小.(II)设AE=y(km),
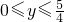 ,总造价为f2(y)万元,
,总造价为f2(y)万元,根据题设有
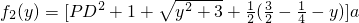 =
=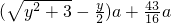 、
、则
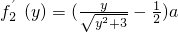 ,由f2′(y)=0,得y=1.
,由f2′(y)=0,得y=1.当y∈(0,1)时,f2′(y)<0,f2(y)在(0,1)内是减函数;
当
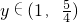 时,f2′(y)>0,f2(y)在
时,f2′(y)>0,f2(y)在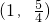 内是增函数.
内是增函数.故当y=1,即AE=1(km)时总造价f2(y)最小,且最小总造价为
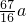 万元.
万元.分析:对于(I)在AB上求一点D,使沿折线PDAO修建公路的总造价最小.这是一个实际应用题,需要先把复杂的图形转化为清晰的几何图形,然后设BD=x(km).根据几何关系列出总造价为f1(x)的函数表达式,再根据配方法求出最小值即为所求.
对于(II)对于(I)中得到的点D,在DA上求一点E,使沿折线PDEO修建公路的总造价最小.设AE=y(km),
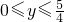 ,总造价为f2(y)万元,求出总造价的f2(y)的函数表达式,求出其导函数的方法,通过判断在区间上正负问题,讨论区间单调性.然后根据单调性求极值即可得到答案.
,总造价为f2(y)万元,求出总造价的f2(y)的函数表达式,求出其导函数的方法,通过判断在区间上正负问题,讨论区间单调性.然后根据单调性求极值即可得到答案.点评:此题主要考查导数的定义及利用导数来求区间函数的最值,利用导数研究函数的单调性和极值、解不等式等基础知识,考查综合分析和解决问题的能力,解题的关键是求导要精确.

练习册系列答案
相关题目
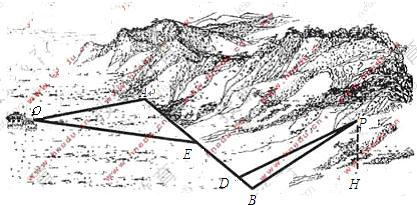
 ,点P到平面α的距离PH=0.4(km)。沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km)。沿山脚原有一段笔直的公路AB可供利用,从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km。当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元。已知OA⊥AB,PB⊥AB,AB=1.5(km),OA=
万元/km。当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元。已知OA⊥AB,PB⊥AB,AB=1.5(km),OA= (km),
(km),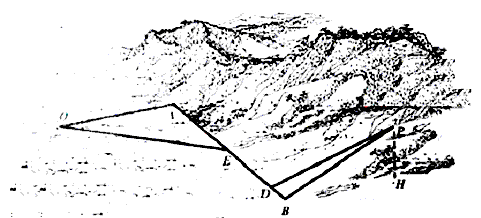

 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),
万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km), .
.