题目内容
已知![]() ,
,![]() 两点,动点P为y轴左侧的点,记点P在x轴上的射影为H,且
两点,动点P为y轴左侧的点,记点P在x轴上的射影为H,且![]() 与
与![]() 分别是公比为2的等比数列的第三、四项。
分别是公比为2的等比数列的第三、四项。
(1)求动点P的轨迹曲线E的方程;
(2)过点(0,-1)的直线l与曲线E交于A、B两点,且|AB|=![]() 若曲线E上存在点C,使
若曲线E上存在点C,使![]() ,求m的值和△ABC的面积S。
,求m的值和△ABC的面积S。
解:设动点P的坐标为(x,y),所以H(x,0)![]() =(0,-y) ,
=(0,-y) ,
![]() =(- 1-x,-y),
=(- 1-x,-y),![]() =( 1-x,-y)
=( 1-x,-y)
![]() =y2;
=y2; ![]() =x2+y2-1 由条件得x2-y2=1
=x2+y2-1 由条件得x2-y2=1
所以所求动点P的轨迹方程为x2-y2=1(x<-1)
(2)显然直线l存在斜率
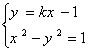 消去y得:(1-k2)x2+2kx-2=0
消去y得:(1-k2)x2+2kx-2=0
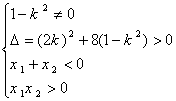 解得:
解得:![]()
(2)|AB|=![]() =2
=2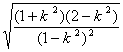 =6
=6![]()
解得:![]() 或
或![]() 又
又![]() 所以
所以![]()
直线AB:![]() x+y+1=0
x+y+1=0
设C(xC,yC)) 由已知![]() 得
得
xC=![]() yC=
yC=![]() 又
又 ![]()
![]()
C(![]() ) 代入双曲线方程:m2=±4 m=-4时所的点在双曲线右支上
) 代入双曲线方程:m2=±4 m=-4时所的点在双曲线右支上
∴ m=4 C(![]() ,2)
,2)
点C到直线AB的距离为![]() ,△ABC的面积S=
,△ABC的面积S=![]() .
.

练习册系列答案
相关题目