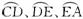题目内容
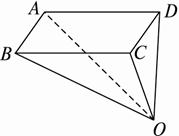
如图2-2-10,ABC—A1B1C1,已知平面平行于三棱锥V-A1B1C1的底面ABC,等边△AB1C所在的平面与底面ABC垂直,且∠ABC=90°,设AC=2a,BC=a.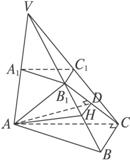
图2-2-10
(1)求证:直线B1C1是异面直线AB1与A1C1的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角A-VB-C的大小.
(1)证明:∵平面A1B1C1∥平面ABC,
∴B1C1∥BC,A1C1∥AC.
∵BC⊥AC,
∴B1C1⊥A1C1.
又∵平面AB1C⊥平面ABC,平面AB1C∩平面ABC=AC,
∴BC⊥平面AB1C.
∴BC⊥AB1.
∴B1C1⊥AB1.
又∵A1C1∩B1C1=C1,B1C1∩AB1=B1.
∴B1C1为AB1与A1C1的公垂线.

(2)解法一:过A作AD⊥B1C于D,
∵△AB1C为正三角形,∴D为B1C的中点.
∵BC⊥平面AB1C,∴BC⊥AD.
又B1C∩BC=C,∴AD⊥平面VBC.
∴线段AD的长即为点A到平面VBC的距离.
在正△AB1C中,AD=![]() ·AC=
·AC=![]() ×2a=
×2a=![]() a,
a,
∴点A到平面VBC的距离为![]() a.
a.
解法二:取AC的中点O,连结B1O,则B1O⊥平面ABC,且B1O=![]() a.
a.
由(1)知BC⊥B1C,设A到平面VBC的距离为x,
∴![]() ,即
,即![]() ×
×![]() BC·AC·B1O=
BC·AC·B1O=![]() ×
×![]() BC·B1C·x,解得x=
BC·B1C·x,解得x=![]() a,
a,
即A到平面VBC的距离为![]() a,则d=||
a,则d=||![]() |·cos〈
|·cos〈![]() ,n〉|=||
,n〉|=||![]() |·
|·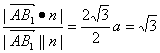 a.
a.
所以,A到平面VBC的距离为![]() a.
a.
(3)解法一:过D点作DH⊥VB于H,连结AH,由三垂线定理知AH⊥VB,
∴∠AHD是二面角A-VB-C的平面角.
在Rt△AHD中,AD=![]() a.△B1DH∽△B1BC.
a.△B1DH∽△B1BC.![]() .
.
∴DH=![]() a.
a.
∴tan∠AHD=![]() .
.
∴∠AHD=arctan![]() .
.
所以,二面角A-VB-C的大小为arctan![]() .
.
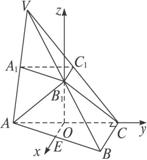
解法二:取AC的中点O,连结B1O,易知OB1⊥底面ABC,过O作直线OE∥BC交AB于E.
取O为空间直角坐标系的原点,OE,OC,OB1所在的直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系.则A(0,-a,0),B(a,a,0),C(0,a,0),B1(0,0,![]() a).
a).
(1)∵![]() =(-a,0,0),
=(-a,0,0),![]() =(0,a,
=(0,a,![]() a),
a),
∴![]() ·
·![]() =(-a,0,0)·(0,a,
=(-a,0,0)·(0,a,![]() a)=0,∴
a)=0,∴![]() ⊥
⊥![]() .∴BC⊥AB1.
.∴BC⊥AB1.
又∵B1C1∥BC,∴B1C1⊥AB1.
由已知BC⊥AC,AC∥A1C1.∴BC⊥A1C1.
而BC∥B1C1,∴B1C1⊥A1C1.
又B1C1与AB1,A1C1显然相交,∴B1C1是AB1与A1C1的公垂线.
(2)设平面VBC的一个法向量n=(x,y,z),
又![]() =(0,-a,
=(0,-a,![]() a),
a),
?由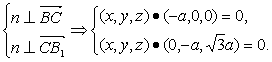
取z=1,得n=(0,![]() ,1),
,1),
点A到平面VBC的距离,即![]() 在平面VBC的法向量n上的投影的绝对值.
在平面VBC的法向量n上的投影的绝对值.
∵![]() =(0,a,
=(0,a,![]() a),∴设所求距离为d,则d=||
a),∴设所求距离为d,则d=||![]() |·cos〈
|·cos〈![]() ,n〉|
,n〉|
=||![]() |·
|·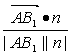 |=
|=![]() =
=![]() a.
a.
∴A到平面VBC的距离为![]() a.
a.
(3)设平面VAB的一个法向量m=(x1,y1,z1),
由由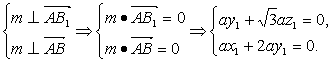
取z1=1,m=(![]() ,1),
,1),
∴cos〈m,n〉=![]() .∵二面角A-VB-C为锐角,
.∵二面角A-VB-C为锐角,
所以二面角A-VB-C的大小为arccos![]() .
.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案