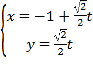题目内容
【题目】已知等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,数列{an}满足a2=4b1,nbn+1-(n+1)bn=n2+n,(n∈N*).
(1)求数列{an}的通项公式;
(2)证明数列{![]() }为等差数列;
}为等差数列;
(3)设数列{cn}的通项公式为:Cn=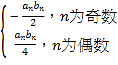 ,其前n项和为Tn,求T2n.
,其前n项和为Tn,求T2n.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)由等比数列的基本量法求解;
(2)求得![]() ,再证
,再证![]() 为常数即可;
为常数即可;
(3)先并项,设![]() ,然后有
,然后有![]() ,用错位相减法计算.
,用错位相减法计算.
(1)由于等比数列{an}的前n项和为Sn,公比q>0,S2=2a2-2,S3=a4-2,
所以S3-S2=a4-2a2=a3,
整理得![]() ,
,
由于a2≠0,
所以q2-q-2=0,由于q>0,
解得q=2.
由于a1+a2=2a2-2,解得a1=2,
所以![]() .
.
(2)数列{an}满足a2=4b1,解得b1=1,
由于nbn+1-(n+1)bn=n2+n,
所以![]() (常数).
(常数).
所以数列数列{![]() }是以1为首项1为公差的等差数列.
}是以1为首项1为公差的等差数列.
(3)由于数列数列{![]() }是以1为首项1为公差的等差数列.
}是以1为首项1为公差的等差数列.
所以![]() ,解得
,解得![]()
由于数列{cn}的通项公式为:Cn=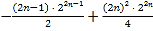 ,
,
所以令![]() =
=![]() =(4n-1)
=(4n-1)![]() 4n-1.
4n-1.
所以![]() ①,
①,
4![]() ②,
②,
①-②得:![]() -(4n-1)
-(4n-1)![]() 4n,
4n,
整理得![]() ,
,
故:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题.
(1)根据以上数据完成下列2×2列联表;
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?
参考公式: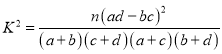 ,其中
,其中![]() .
.