Question

已知A＝{x|x²≥9}，B＝{x|≤0}，C＝{x||x－2|＜4}．

(1)求A∩B及A∪C；

(2)若U＝R，求A∩?_U(B∩C)

 

Answer 1

【答案】

(1)A∩B＝{x|3≤x≤7}，．A∪C＝{x|x≤－3，或x＞－2}，．

(2)A∩?_U(B∩C)＝{x|x≥6或x≤－3}

【解析】

试题分析：由x²≥9，得x≥3，或x≤－3，

∴A＝{x|x≥3，或x≤－3}．

又由不等式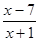≤0，得－1＜x≤7，

∴B＝{x|－1＜x≤7}．

又由|x－2|＜4，得－2＜x＜6，∴C＝{x|－2＜x＜6}．

(1)A∩B＝{x|3≤x≤7}，．A∪C＝{x|x≤－3，或x＞－2}，．

(2)∵U＝R，B∩C＝{x|－1＜x＜6}，

∴?_U(B∩C)＝{x|x≤－1或x≥6}，

∴A∩?_U(B∩C)＝{x|x≥6或x≤－3}

考点：本题主要考查集合的运算，简单不等式解法。

点评：典型题，这类题目在高考题中很难出现，但平时训练题中多有，有一定的综合性。进行的运算，首先应明确集合中元素或元素特征。