题目内容
设全集U=R，P={m|方程mx2-4x+1=0有实数根}，N={x|2x＜8}，求P∩（CUN）．
解：当m=0时，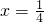
，符合题意…
当m≠0时，方程mx2-4x+1=0有实数根，则△=16-4m≥0
即m≤4且m≠0
综上可知P={m|m≤4}…
又∵N={x|2x＜8}
∴N={x|x＜3}…
∴CUN={x|x≥3}…
∴P∩（CuN）={x|3≤x≤4}…
分析：由已知中P={m|方程mx2-4x+1=0有实数根}，我们分m=0，此时方程为一次方程，m≠0，此时方程为二次方程，求出满足条件的集合P，N={x|2x＜8}，解指数不等式可以求出满足条件的集合N，进而由集合的交集和补集运算法则，即可得到答案．
点评：本题考查的知识点是指数函数的单调性的应用，集合的交、并、补集运算，其中求出集合P，N是解答本题的关键，在解答集合P时，易忽略m=0的情况．
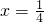，符合题意…当m≠0时，方程mx2-4x+1=0有实数根，则△=16-4m≥0
即m≤4且m≠0
综上可知P={m|m≤4}…
又∵N={x|2x＜8}
∴N={x|x＜3}…
∴CUN={x|x≥3}…
∴P∩（CuN）={x|3≤x≤4}…
分析：由已知中P={m|方程mx2-4x+1=0有实数根}，我们分m=0，此时方程为一次方程，m≠0，此时方程为二次方程，求出满足条件的集合P，N={x|2x＜8}，解指数不等式可以求出满足条件的集合N，进而由集合的交集和补集运算法则，即可得到答案．
点评：本题考查的知识点是指数函数的单调性的应用，集合的交、并、补集运算，其中求出集合P，N是解答本题的关键，在解答集合P时，易忽略m=0的情况．
练习册系列答案
相关题目