题目内容
已知点P(x,y)对应的复数z满足|z|=1,则点Q(x+y,xy)的轨迹是( )
| A、圆 | B、抛物线的一部分 | C、椭圆 | D、双曲线的一部分 |
分析:根据复数的模|z|=
,把点P(x,y)对应的复数z满足|z|=1,再利用配方法,即可求得点Q(x+y,xy)的轨迹,注意纵坐标的范围.
| x2+y2 |
解答:解:由题意知x2+y2=1,∴(x+y)2-2xy=1.
令x+y=m,xy=n,则有m2-2n=1,∴m2=2n+1.
又∵2|xy|≤x2+y2=1,∴-
≤n≤
.
∴点Q的轨迹是抛物线的一部分.
故选B.
令x+y=m,xy=n,则有m2-2n=1,∴m2=2n+1.
又∵2|xy|≤x2+y2=1,∴-
| 1 |
| 2 |
| 1 |
| 2 |
∴点Q的轨迹是抛物线的一部分.
故选B.
点评:考查代入法求轨迹方程,抛物线的方程和复数模的运算,在计算过程中注意整体代换,和利用基本不等式求坐标的范围,增加了题目的难度,属中档题.

练习册系列答案
相关题目
 上一点,F1、F2为椭圆左、右焦点,下列结论中:①△PF1F2面积的最大值为
上一点,F1、F2为椭圆左、右焦点,下列结论中:①△PF1F2面积的最大值为 ;②若过点P、F2的直线l与椭圆的另一交点为Q,则△PF1Q的周长为8;③若过点P、F2的直线l与椭圆的另一交点为Q,则恒有
;②若过点P、F2的直线l与椭圆的另一交点为Q,则△PF1Q的周长为8;③若过点P、F2的直线l与椭圆的另一交点为Q,则恒有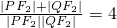 ;对定点
;对定点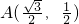 ,则
,则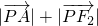 的取值范围为
的取值范围为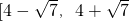 .其中正确结论的番号是________.
.其中正确结论的番号是________. ”.类比这一结论,我们猜想:“若曲线C的方程为
”.类比这一结论,我们猜想:“若曲线C的方程为 (如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.
(如图),则xE•xF也是与点M、N、P位置无关的定值”,请你对该猜想给出证明.