Question

（05年浙江卷理）（14分）

如图，已知椭圆的中心在坐标原点，焦点F₁，F₂在x轴上，长轴A₁A₂的长为4，左准线l与x轴的交点为M，|MA₁|∶|A₁F₁|＝2∶1．

   (Ⅰ)求椭圆的方程；

   (Ⅱ)若直线l₁：x＝m(|m|＞1)，P为l₁上的动点，使∠F₁PF₂最大的点P记为Q，求点Q的坐标(用m表示)．

Answer 1

解析：(Ⅰ)设椭圆的方程为(a>0,b>0),半焦距为c,则|MA₁|=,|A₁F₁|=a-c
由题意,得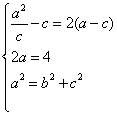∴a=2,b=,c=1.

故椭圆的方程为

(Ⅱ)设P(m,y_q),|m|>1,

当y_q=0时,∠F₁PF₂=0,当y_q≠0时,0<∠F₁PF₂<∠PF₁M<,

∴只需求tan∠F₁PF₂的最大值即可.

设直线PF₁的斜率k₁=,直线PF₂的斜率k₂=,

∴tan∠F₁PF₂=

当且仅当时,∠F₁PF₂最大,∴Q(m,),|m|>1