题目内容
19.设函数g(x)=Asin(ωx+φ)+B(A>0,ω>0),满足:当x1,x2∈R时,有|g(x1)-g(x2)|≤$\frac{1}{4}$,当相位为$\frac{π}{6}$时,g(x)的值为$\frac{7}{16}$.(1)当g(x)的周期为π,初相为$\frac{π}{3}$,且g(x)≥$\frac{1}{2}$时,求x的范围;
(2)若f(x)=ax-$\frac{3}{2}$x2的最大值不大于$\frac{1}{6}$,且f(g(x))≥$\frac{1}{8}$,求a的值.
分析 (1)由已知分别求出A,ω,φ,B的值,可得函数的解析式,结合g(x)≥$\frac{1}{2}$,可得满足条件的x的范围;
(2)令t=g(x),则t∈[$\frac{1}{4}$,$\frac{1}{2}$],则f(t)≥$\frac{1}{8}$,t∈[$\frac{1}{4}$,$\frac{1}{2}$],结合f(x)=ax-$\frac{3}{2}$x2的最大值不大于$\frac{1}{6}$,可得$\left\{\begin{array}{l}\frac{{a}^{2}}{6}≤\frac{1}{6}\\-\frac{3}{32}+\frac{1}{4}a≥\frac{1}{8}\\-\frac{3}{8}+\frac{1}{2}a≥\frac{1}{8}\end{array}\right.$,解得答案.
解答 解:(1)∵T=$\frac{2π}{ω}$=π,
∴ω=2,
∵初相为$\frac{π}{3}$,
φ=$\frac{π}{3}$,
∵当x1,x2∈R时,有|g(x1)-g(x2)|≤$\frac{1}{4}$,
∴A=$\frac{1}{8}$,
∵当相位为$\frac{π}{6}$时,g(x)的值为$\frac{7}{16}$,
∴$\frac{1}{8}$sin$\frac{π}{6}$+B=$\frac{7}{16}$,
∴B=$\frac{3}{8}$,
∴g(x)=$\frac{1}{8}$sin(2x+$\frac{π}{3}$)+$\frac{3}{8}$,
∴g(x)≥$\frac{1}{2}$,即
$\frac{1}{8}$sin(2x+$\frac{π}{3}$)+$\frac{3}{8}$$≥\frac{1}{2}$,
∴sin(2x+$\frac{π}{3}$)≥1,
∵sin(2x+$\frac{π}{3}$)≤1,
∴sin(2x+$\frac{π}{3}$)=1
∴2x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,
∴x=$\frac{π}{12}$+kπ,k∈Z,
∴{x|x=$\frac{π}{12}$+kπ,k∈Z},
(2)令t=g(x),则t∈[$\frac{1}{4}$,$\frac{1}{2}$],
∵f(x)=ax-$\frac{3}{2}$x2的最大值不大于$\frac{1}{6}$,f(t)≥$\frac{1}{8}$,t∈[$\frac{1}{4}$,$\frac{1}{2}$],
∴$\left\{\begin{array}{l}\frac{{a}^{2}}{6}≤\frac{1}{6}\\-\frac{3}{32}+\frac{1}{4}a≥\frac{1}{8}\\-\frac{3}{8}+\frac{1}{2}a≥\frac{1}{8}\end{array}\right.$,
解得:a=1
点评 本题主要考查了函数f(x)=Asin(ωx+φ)的图象和性质,利用正弦函数图象和性质求三角函数值域的方法,属中档题.

 某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测加工10个零件需要多少时间?(注:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| A. | M=N | B. | M∩N=∅ | C. | M⊆N | D. | N?M |
 已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.
已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.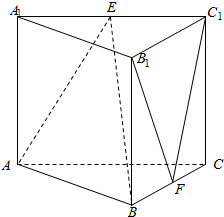 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明:
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明: