题目内容
平面向量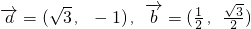 ,若存在不同时为0的实数k和t,使
,若存在不同时为0的实数k和t,使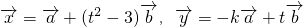 ,且
,且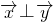 ,试确定函数k=f(t)的单调区间.
,试确定函数k=f(t)的单调区间.
解:由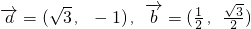 得,
得,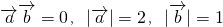 .
.
再由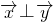 可得
可得 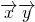 =
=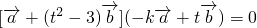 ,
,
即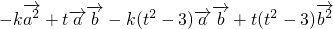 =0.
=0.
故有-4k+t3-3t=0,k= (t3-3t ),故 f(t)=
(t3-3t ),故 f(t)= (t3-3t ).
(t3-3t ).
由 f′(t)= t2-
t2- >0,解得 t<-1,或 t>1.
>0,解得 t<-1,或 t>1.
令f′(t)= t2-
t2- <0,解得-1<t<1.
<0,解得-1<t<1.
所以f(t)的增区间为(-∞,-1)、(1,+∞);减区间为(-1,1).
分析:利用两个向量垂直的性质可得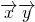 =
=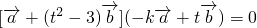 ,化简求得 k=
,化简求得 k= (t3-3t ),
(t3-3t ),
故 f(t)= (t3-3t ),利用导数求函数f(t) 的单调区间.
(t3-3t ),利用导数求函数f(t) 的单调区间.
点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,利用导数求函数的单调区间,属于中档题.
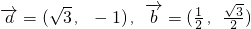 得,
得,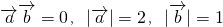 .
.再由
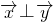 可得
可得 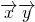 =
=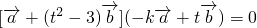 ,
,即
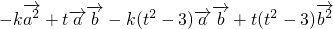 =0.
=0.故有-4k+t3-3t=0,k=
 (t3-3t ),故 f(t)=
(t3-3t ),故 f(t)= (t3-3t ).
(t3-3t ).由 f′(t)=
 t2-
t2- >0,解得 t<-1,或 t>1.
>0,解得 t<-1,或 t>1.令f′(t)=
 t2-
t2- <0,解得-1<t<1.
<0,解得-1<t<1.所以f(t)的增区间为(-∞,-1)、(1,+∞);减区间为(-1,1).
分析:利用两个向量垂直的性质可得
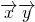 =
=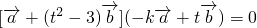 ,化简求得 k=
,化简求得 k= (t3-3t ),
(t3-3t ),故 f(t)=
 (t3-3t ),利用导数求函数f(t) 的单调区间.
(t3-3t ),利用导数求函数f(t) 的单调区间.点评:本题主要考查两个向量的数量积的运算,两个向量垂直的性质,利用导数求函数的单调区间,属于中档题.

练习册系列答案
相关题目
 (2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且
(2013•嘉定区二模)如图,已知点F(0,1),直线m:y=-1,P为平面上的动点,过点P作m的垂线,垂足为点Q,且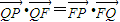 .
.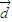 =(a,1)的直线m′与轨迹C交于不同两点A、B,问是否存在实数a使得FA⊥FB?若存在,求出a的范围;若不存在,请说明理由;
=(a,1)的直线m′与轨迹C交于不同两点A、B,问是否存在实数a使得FA⊥FB?若存在,求出a的范围;若不存在,请说明理由;