题目内容
已知椭圆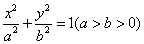 的一条准线为
的一条准线为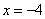 ,且与抛物线
,且与抛物线 有相同的焦点.
有相同的焦点.
(Ⅰ)求椭圆的方程;
(Ⅱ)设点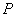 是该椭圆的左准线与
是该椭圆的左准线与 轴的交点,是否存在过点
轴的交点,是否存在过点 的直线
的直线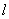 与椭圆相交于
与椭圆相交于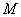 、
、 两点,且线段
两点,且线段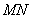 的中点恰好落到由该椭圆的两个焦点、两个短轴顶点所围成的四边形区域内(包括边界)?若存在,求出直线
的中点恰好落到由该椭圆的两个焦点、两个短轴顶点所围成的四边形区域内(包括边界)?若存在,求出直线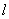 的斜率的取值范围;若不存在,请说明理由.
的斜率的取值范围;若不存在,请说明理由.
【答案】
解:(Ⅰ)依题意,易知椭圆的方程为 .
.
…………4分
.
.
…………4分
(Ⅱ)椭圆的左准线方程为 ,点P的坐标
,点P的坐标 ,
,
假设存在直线 符合题意,其斜率
符合题意,其斜率 显然存在,设直线
显然存在,设直线 的方程为
的方程为 . ………5分
. ………5分
设点 的坐标分别为
的坐标分别为 线段
线段 的中点为
的中点为 ,
,
将 代入椭圆,得
代入椭圆,得 .……①
………6分
.……①
………6分
由 解得
解得 .……②
…………7分
.……②
…………7分
 ,于是
,于是 ,
,
因为 ,所以点
,所以点 不可能在
不可能在 轴的右边, …………9分
轴的右边, …………9分
又直线 ,方程分别为
,方程分别为 ,则必有
,则必有
 即
即 亦即
亦即 . …………11分
. …………11分
解得 ,此时②也成立.
…………12分
,此时②也成立.
…………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

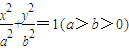 的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.
的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.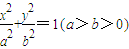 的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.
的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.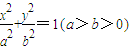 的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.
的一条准线为x=-4,且与抛物线y2=8x有相同的焦点.