题目内容
若A为不等式组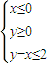
表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为（ ）A．
B．1
C．
D．2
【答案】分析：本题主要考查线性规划的基本知识，先画出约束条件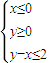
的可行域，再分析当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的形状，然后代入相应的公式，求出区域的面积．
解答：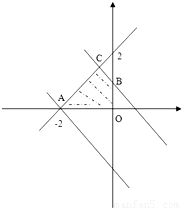
解析：作出可行域，如图，
则直线扫过的面积为
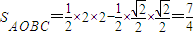
故选C．
点评：平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．
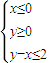的可行域，再分析当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的形状，然后代入相应的公式，求出区域的面积．解答：
解析：作出可行域，如图，则直线扫过的面积为
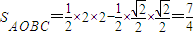
故选C．
点评：平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．
练习册系列答案
阅读快车系列答案
相关题目
表示的平面区域，则当
变化到1时，动直线
扫过A中的那部分区域的面积为；
B．1 C．
D．2
表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为（ ）
表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为（ ）
表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为（ ）
表示的平面区域，则当a从-2连续变化到1时，动直线x+y=a扫过A中的那部分区域的面积为（ ）
