题目内容
已知椭圆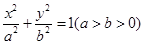 的离心率为
的离心率为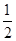 ,且经过点
,且经过点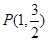 . 过它的两个焦点
. 过它的两个焦点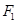 ,
, 分别作直线
分别作直线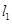 与
与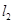 ,
,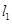 交椭圆于A、B两点,
交椭圆于A、B两点,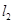 交椭圆于C、D两点,且
交椭圆于C、D两点,且 .
.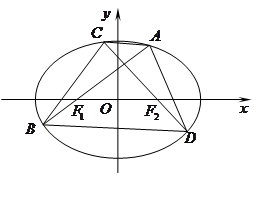
(1)求椭圆的标准方程;
(2)求四边形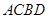 的面积
的面积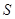 的取值范围.
的取值范围.
(1)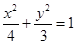 ;(2)
;(2)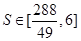
解析试题分析:(1)由离心率为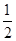 可知
可知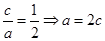 ,所以
,所以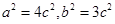 ,再将点P的坐标代入椭圆方程得
,再将点P的坐标代入椭圆方程得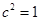 ,故所求椭圆方程为
,故所求椭圆方程为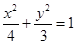 ;
;
(2)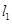 与
与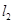 垂直,可分为两种情况讨论:一是当
垂直,可分为两种情况讨论:一是当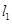 与
与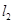 中有一条直线的斜率不存在,则另一条直线的斜率为0;二是若
中有一条直线的斜率不存在,则另一条直线的斜率为0;二是若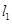 与
与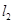 的斜率都存在;
的斜率都存在;
当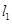 与
与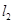 中有一条直线的斜率不存在,则另一条直线的斜率为0,此时四边形的面积为
中有一条直线的斜率不存在,则另一条直线的斜率为0,此时四边形的面积为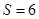 ;
;
若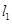 与
与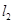 的斜率都存在,设
的斜率都存在,设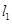 的斜率为
的斜率为 ,则
,则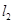 的斜率为
的斜率为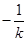 .
. 直线
直线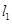 的方程为
的方程为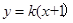 ,
,
设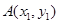 ,
,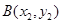 ,联立
,联立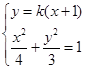 ,消去
,消去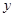 整理得,
整理得,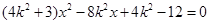
(1)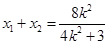 ,
,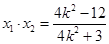 ,
, 
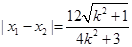 ,
,
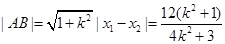
(2),注意到方程(1)的结构特征,或图形的对称性,可以用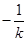 代替(2)中的
代替(2)中的 ,
,
得 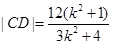 ,
, 
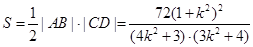 ,利用换元法,再利用对构函数可以求出最值,令
,利用换元法,再利用对构函数可以求出最值,令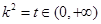 ,
,
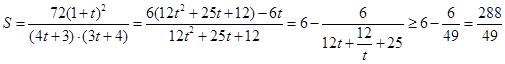 ,
, 
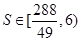 ,综上可知,四边形
,综上可知,四边形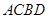 面积的
面积的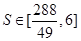 .
.
试题解析:(1)由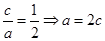 ,所以
,所以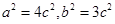 , 2分
, 2分
将点P的坐标代入椭圆方程得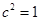 , 4分
, 4分
故所求椭圆方程为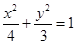 5分
5分
(2)当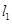 与
与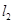 中有一条直线的斜率不存在,则另一条直线的斜率为0,
中有一条直线的斜率不存在,则另一条直线的斜率为0,
此时四边形的面积为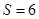 , 7分
, 7分
若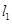 与
与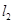 的斜率都存在,设
的斜率都存在,设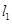 的斜率为
的斜率为 ,则
,则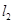 的斜率为
的斜率为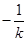 .
. 直线
直线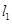 的方程为
的方程为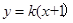 ,
,
设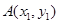 ,
,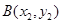 ,联立
,联立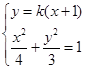 ,
,
消去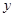 整理得,
整理得,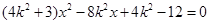

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
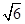 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: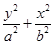 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=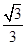 ,直线l被圆O截得的弦长与椭圆的短轴长相等.
,直线l被圆O截得的弦长与椭圆的短轴长相等.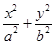 =1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.
=1(a>b>0)的一个顶点,C1的长轴是圆C2:x2+y2=4的直径.l1,l2是过点P且互相垂直的两条直线,其中l1交圆C2于A,B两点,l2交椭圆C1于另一点D.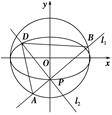
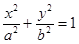 (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,斜率为1的直线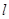 与椭圆C交于不同两点M,N.
与椭圆C交于不同两点M,N.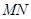 的长;
的长;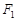 、
、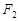 为双曲线
为双曲线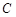 :
: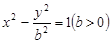 的左、右焦点,过
的左、右焦点,过 轴的直线,在
轴的直线,在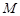 ,且
,且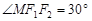 .圆
.圆 的方程是
的方程是 .
.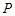 作该双曲线两条渐近线的垂线,垂足分别为
作该双曲线两条渐近线的垂线,垂足分别为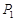 、
、 ,求
,求 的值;
的值; =1(a>b>0)上两点,已知m=
=1(a>b>0)上两点,已知m=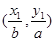 ,n=
,n=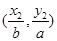 ,若m·n=0且椭圆的离心率e=
,若m·n=0且椭圆的离心率e= ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.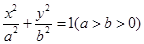 的右焦点为F2(1,0),点
的右焦点为F2(1,0),点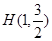 在椭圆上.
在椭圆上.
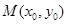 在圆
在圆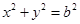 上,M在第一象限,过M作圆
上,M在第一象限,过M作圆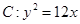 ,点
,点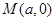 ,过
,过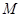 的直线
的直线 交抛物线
交抛物线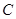 于
于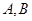 两点.
两点.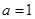 ,抛物线
,抛物线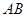 中点的连线垂直于
中点的连线垂直于 轴,求直线
轴,求直线 为小于零的常数,点
为小于零的常数,点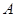 关于
关于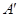 ,求证:直线
,求证:直线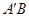 过定点
过定点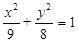 的焦点为焦点,且过
的焦点为焦点,且过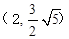 点的双曲线的标准方程.
点的双曲线的标准方程.