题目内容
甲、乙两人玩投篮游戏,规则如下:两人轮流投篮,每人至多投2次,甲先投,若有人投中即停止投篮,结束游戏,已知甲每次投中的概率为
,乙每次投中的概率为
求:
(I)乙投篮次数不超过1次的概率.
(Ⅱ)记甲、乙两人投篮次数和为ξ,求ξ的分布列和数学期望.
| 1 |
| 4 |
| 1 |
| 3 |
(I)乙投篮次数不超过1次的概率.
(Ⅱ)记甲、乙两人投篮次数和为ξ,求ξ的分布列和数学期望.
(I)记“甲投篮投中”为事件A,“乙投篮投中”为事件B.
“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,
所求的概率是P=P(A+
?B+
?
?A)
=P(A)+P(
?B)+P(
?
?A)=P(A)+P(
)?P(B)+P(
)?P(
)?P(A)
乙投篮次数不超过1次的概率为
…(7分)
(2)甲、乙投篮总次数ξ的取值1,2,3,4,
甲、乙投篮次数总和ξ的分布列为:
…(11分)
甲、乙投篮总次数ξ的数学期望为Eξ=1×
+2×
+3×
+4×
=
…(13分)
“乙投篮次数不超过1次”包括三种情况:一种是甲第1次投篮投中,另一种是甲第1次投篮未投中而乙第1次投篮投中,再一种是甲、乙第1次投篮均未投中而甲第2次投篮投中,
所求的概率是P=P(A+
| . |
| A |
| . |
| A |
| . |
| B |
=P(A)+P(
| . |
| A |
| . |
| A |
| . |
| B |
| . |
| A |
| . |
| A |
| . |
| B |
|
乙投篮次数不超过1次的概率为
| 5 |
| 8 |
(2)甲、乙投篮总次数ξ的取值1,2,3,4,
甲、乙投篮次数总和ξ的分布列为:
| ξ | 1 | 2 | 3 | 4 | ||||||||
| P |
|
|
|
|
甲、乙投篮总次数ξ的数学期望为Eξ=1×
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 8 |
| 3 |
| 8 |
| 21 |
| 8 |

练习册系列答案
相关题目
 ,乙每次投中的概率为
,乙每次投中的概率为 。
。 ,乙每次投中的概率为
,乙每次投中的概率为 求:
求: ,乙每次投中的概率为
,乙每次投中的概率为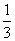 。
。 ,求
,求