题目内容
甲、乙两人玩投篮游戏,规则如下:
两人轮流投篮,每人至多投2次,甲先投,若有人投中则立即停止投篮,结束游戏,已知甲每次投中的概率为 ,乙每次投中的概率为
,乙每次投中的概率为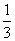 。
。
(I)求乙投篮次数不超过1次的概率;
(Ⅱ)甲、乙两人投篮次数的和为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
【答案】
解:(I)记甲投中为事件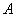 ,乙投中为事件
,乙投中为事件 。
。
所以
因为“乙投篮次数不超过1次”的对立事件是“乙投篮2次”,
故所求的概率是
答:乙投篮次数不超过1次的概率为
(Ⅱ)因为甲、乙投篮总次数 的取值为1,2,3,4,
的取值为1,2,3,4,
所以

甲、乙投篮次数总和 的分布列为
的分布列为
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
|
甲、乙投篮总次数 的数学期望为
的数学期望为
答:甲、乙投篮次数总和 的数学期望为
的数学期望为 。
。

练习册系列答案
相关题目
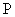
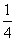


 ,乙每次投中的概率为
,乙每次投中的概率为 。
。 ,乙每次投中的概率为
,乙每次投中的概率为 求:
求: