题目内容
（1）已知x，y，z∈R，且x+y+z=8，x2+y2+z2=24，求证：
≤x≤4，
≤y≤4，
≤z≤4．
（2）已知a1，b1，x1，x2∈R+，ab=1，x1+x2=2，求证：（ax1+bx2）（bx1+ax2）≥4
（3）已知a．b．c．d∈R+且a+b+c+d=1，求证：
+
+
+
≥16．
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
（2）已知a1，b1，x1，x2∈R+，ab=1，x1+x2=2，求证：（ax1+bx2）（bx1+ax2）≥4
（3）已知a．b．c．d∈R+且a+b+c+d=1，求证：
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
分析：（1）用x表示y+z和y2+z2，即y+z=8-x，y2+z2=24-x2．再利用柯西不等式（y2+z2）（1+1）≥（y+z）2
得到关于x的一元二次不等式（24-x2）（1+1）≥（8-x）2，化简求得x的范围即可，同理可求得y和z的范围
（2）直接利用柯西不等式(ax1+bx2)(bx1+ax2)≥(
•
+
•
) 2证明得到；
（3）直接利用柯西不等式(
+
+
+
)(a+b+c+d)≥(1+1+1+1)2=16证明得到．
得到关于x的一元二次不等式（24-x2）（1+1）≥（8-x）2，化简求得x的范围即可，同理可求得y和z的范围
（2）直接利用柯西不等式(ax1+bx2)(bx1+ax2)≥(
| ax1 |
| bx1 |
| bx2 |
| ax2 |
（3）直接利用柯西不等式(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
解答：证明：（1）∵x，y，z∈R，x+y+z=8，x2+y2+z2=24，∴y+z=8-x，y2+z2=24-x2．
又由柯西不等式可知（y2+z2）（1+1）≥（y+z）2，即（24-x2）（1+1）≥（8-x）2，
化简后可得
≤x≤4，同理可证
≤y≤4，
≤z≤4．
（2）∵a1，b1，x1，x2∈R+，ab=1，x1+x2=2，
∴(ax1+bx2)(bx1+ax2)≥(
•
+
•
) 2=（x1+x2）2=4．
∴（ax1+bx2）（bx1+ax2）≥4．
（3）∵a．b．c．d∈R+a+b+c+d=1，
∴(
+
+
+
)(a+b+c+d)≥(1+1+1+1)2=16．
又由柯西不等式可知（y2+z2）（1+1）≥（y+z）2，即（24-x2）（1+1）≥（8-x）2，
化简后可得
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
（2）∵a1，b1，x1，x2∈R+，ab=1，x1+x2=2，
∴(ax1+bx2)(bx1+ax2)≥(
| ax1 |
| bx1 |
| bx2 |
| ax2 |
∴（ax1+bx2）（bx1+ax2）≥4．
（3）∵a．b．c．d∈R+a+b+c+d=1，
∴(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
点评：此题考查柯西不等式应用．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
．
．
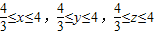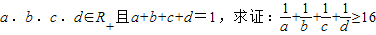