题目内容
厚度均匀的圆柱形金属饮料罐容积一定时，它的高与底面半径的比为（ ），才能使材料最省？A．
B．2
C．
D．3
【答案】分析：解：设圆柱的底面半径r，高h容积为v，则v=πr2h 
要求用料最省即圆柱的表面积最小，由题意可得 S=
，配凑基本不等式的形式，从而求最小值，从而可求高与底面半径之比
解答：解：设圆柱的底面半径r，高h容积为v
v=πr2h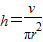
S=
=
•πr
当且仅当
即
时S最小即用料最省
此时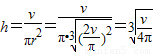
∴
故选A
点评：本题主要考查了基本不等式在最值求解中的应用，利用基本不等式的关键是要符合其形式，并且要注意验证等号成立的条件．
要求用料最省即圆柱的表面积最小，由题意可得 S=
，配凑基本不等式的形式，从而求最小值，从而可求高与底面半径之比解答：解：设圆柱的底面半径r，高h容积为v
v=πr2h
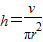
S=
=
•πr当且仅当
即时S最小即用料最省此时
∴
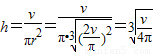
故选A
点评：本题主要考查了基本不等式在最值求解中的应用，利用基本不等式的关键是要符合其形式，并且要注意验证等号成立的条件．
练习册系列答案
相关题目
厚度均匀的圆柱形金属饮料罐容积一定时，它的高与底面半径的比为（ ），才能使材料最省？
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |