题目内容
设函数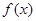 的定义域为
的定义域为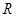 ,对任意的实数
,对任意的实数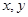 都有
都有 ;当
;当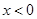 时,
时,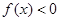 ,且
,且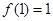 .(1)判断并证明
.(1)判断并证明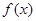 在
在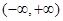 上的单调性;
上的单调性;
(2)若数列 满足:
满足: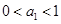 ,且
,且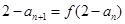 ,证明:对任意的
,证明:对任意的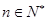 ,
,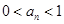
【答案】
(1)单调递增(2)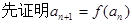 ,再利用
,再利用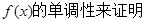 .
.
【解析】
试题分析:(1)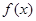 在
在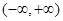 上单调递增,证明如下: 设任意
上单调递增,证明如下: 设任意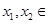
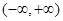 ,且
,且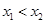 ,∵
,∵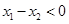 ,∴
,∴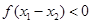 ,∴
,∴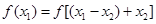
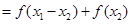
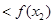
即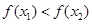 ,∴
,∴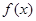 在
在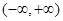 上单调递增.
上单调递增.
(2)在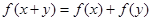 中,令
中,令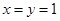 ,得
,得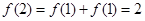 .令
.令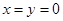 ,
,
得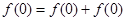 ,∴
,∴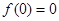 .令
.令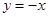 ,得
,得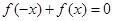 ,即
,即

下面用数学归纳法证明:
①当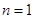 时,
时, ,不等式成立;
,不等式成立;
②假设当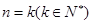 时,不等式成立,即
时,不等式成立,即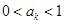 ,则∵
,则∵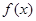 在
在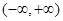 上单调递增,
上单调递增,
∴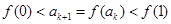 ,∴
,∴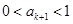 ,即当
,即当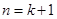 时不等式也成立.
时不等式也成立.
综上①②,由数学归纳法原理可知对任意的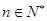 ,
,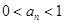
考点:数学归纳法;抽象函数及其应用;数列与函数的综合
点评:本题考查函数的单调性,考查数学归纳法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 的定义域为R,当
的定义域为R,当 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有 成立,数列
成立,数列 满足
满足 且
且
 的值;
的值; 对一切
对一切 均成立,求
均成立,求 的最大值.
的最大值. 的定义域为R,当
的定义域为R,当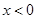 时,
时, ,且对任意实数
,且对任意实数 ,都有
,都有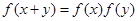 成立,数列
成立,数列 满足
满足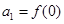 且
且
 的值;
的值;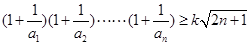 对一切
对一切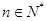 均成立,求
均成立,求 的最大值.
的最大值.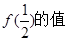 ;
;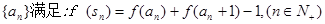 其中sn是数列
其中sn是数列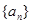 的前n项和,求
的前n项和,求