题目内容
设函数
 的最小正周期为
的最小正周期为 ,且
,且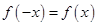 ,则( )
,则( )
A. 在 在 单调递减 单调递减 | B. 在 在 单调递减 单调递减 |
C. 在 在 单调递增 单调递增 | D. 在 在 单调递增 单调递增 |
A
解析试题分析:
根据题意,由于函数
 的最小正周期为
的最小正周期为 ,故可知
,故可知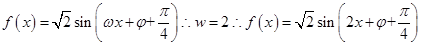 ,又因为
,又因为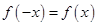 ,则可知函数为偶函数,因此可知
,则可知函数为偶函数,因此可知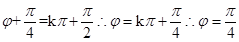 ,因此可知
,因此可知 ,那么可知在
,那么可知在 单调递减,选A.
单调递减,选A.
考点:三角函数的单调性
点评:解决该试题的关键是利用三角函数的周期公式和函数的偶函数性质得到参数的值,进而分析其单调区间,属于基础题。

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
时间经过2h,时针转过的角是( )
A. | B. | C.2π | D. π π |
如图,量角器外缘边上有A,P,Q三点,它们所表示的读数分别是180°,70°,30°,则∠PAQ的大小为 【 】
| A.10° | B.20° | C.30° | D.40° |
将函数 的图象向左平移
的图象向左平移 个单位,得到函数
个单位,得到函数 的图象.若
的图象.若 在[
在[ ]上为增函数,则
]上为增函数,则 的最大值为
的最大值为
| A.4 | B.3 | C.2 | D.1 |
终边在一、三象限角平分线的角的集合是 ( )
A. | B. |
C. | D. |
函数 在一个周期内的图象如下,此函数的解析式为可为( ).
在一个周期内的图象如下,此函数的解析式为可为( ).
A. | B. |
C. | D. |
在 内,使
内,使 成立的
成立的 的取值范围是 ( )
的取值范围是 ( )
A. | B.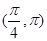 |
C. | D.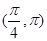  |
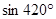 的值是 ( )
的值是 ( )
A.-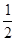 | B.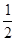 | C.-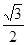 | D.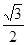 |
已知 ∈(
∈(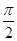 ,
, ),sin
),sin =
= ,则tan(
,则tan( )等于
)等于
| A.-7 | B.-  | C.7 | D. |