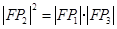题目内容
(12分)已知抛物线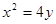 的焦点为
的焦点为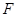 ,准线为
,准线为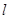 ,过
,过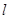 上一点P作抛物线的两切线,切点分别为A、B,
上一点P作抛物线的两切线,切点分别为A、B,
(1)求证: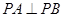 ;
;
(2)求证:A、F、B三点共线;
(3)求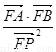 的值.
的值.
【答案】
(3)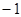
【解析】
试题分析:(1)准线为y=-1,F(0,1),设P(n,-1),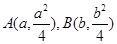 ,
,
因为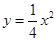 ,所以
,所以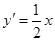 ,
,
所以 ,即
,即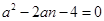 ,
,
 ,即
,即 ,
,
所以a,b是方程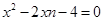 ,
,
所以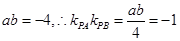 ,
,
所以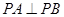 .
.
(2)由(1)知a+b=2n,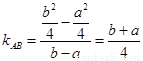 ,
,
所以直线AB的方程为 即
即
因为a+b=2n,ab=-4,所以直线AB的方程为 ,
,
所以恒过点F(0,1).
(3)
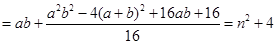 ,
,
因为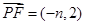 ,所以
,所以 ,
,
所以
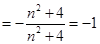 为常数.
为常数.
考点:直线与抛物线的相切,直线的斜率,导数的几何意义,向量的数量积.
点评:根据导数的几何意义,分别求出切点A,B处的导数即A,B的斜率,然后证明斜率之积为-1,来证明两条切线垂直.证明A,B,F三点共线,关键是利用第(1)问的结果,求出AB的点方程,证明点F的坐标满足此方程即可.第(3)问分别求出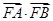 和
和 都用n表示,从而证明其为定值.
都用n表示,从而证明其为定值.

练习册系列答案
相关题目
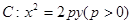 的焦点为
的焦点为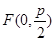 ,准线为
,准线为 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为 .
.
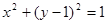 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交 轴于点
轴于点 ,求
,求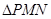 面积的最小值时
面积的最小值时 的值.
的值. 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有 ( )
, 则有 ( ) B.
B.
 D.
D.
 的焦点为
的焦点为 ,
, 过
过 轴的垂线交抛物线于
轴的垂线交抛物线于 两点.有下列四个命题:①
两点.有下列四个命题:① 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在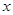 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 ,则有( )
,则有( ) B.
B.
 D.
D.