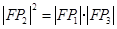题目内容
已知抛物线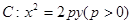 的焦点为
的焦点为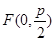 ,准线为
,准线为 ,点
,点 为抛物线C上的一点,且
为抛物线C上的一点,且 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为 .
.

(I)求抛物线C的方程;
(II)若圆F的方程为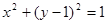 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交 轴于点
轴于点 ,求
,求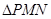 面积的最小值时
面积的最小值时 的值.
的值.
【答案】
(I)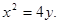 ;(II)
;(II)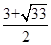 .
.
【解析】
试题分析:(I)先求圆心纵坐标,再由圆心到准线的距离,可求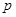 的值,从而得抛物线的方程;(II)先设过点
的值,从而得抛物线的方程;(II)先设过点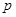 斜率存在的直线方程,根据直线与圆
斜率存在的直线方程,根据直线与圆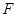 相切,可得两切线的斜率关系,然后得
相切,可得两切线的斜率关系,然后得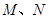 两点坐标,可得
两点坐标,可得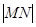 ,然后再求三角形PMN的面积,再利用导数判断面积的单调性而求最小值,再得
,然后再求三角形PMN的面积,再利用导数判断面积的单调性而求最小值,再得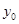 的值.
的值.
试题解析:(I)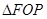 的外接圆的圆心在直线OF,FP的中垂线交点上,且直线OF的中垂线为直线
的外接圆的圆心在直线OF,FP的中垂线交点上,且直线OF的中垂线为直线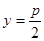 ,则圆心的纵坐标为
,则圆心的纵坐标为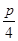 ,
1分
,
1分
故到准线的距离为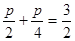 . 2分
. 2分
从而p=2,即C的方程为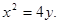 .
5分
.
5分
(II)设过点P斜率存在的直线为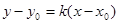 ,则点F(0,1)到直线的距离
,则点F(0,1)到直线的距离
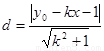 。
7分
。
7分
令d=1,则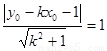 ,所以
,所以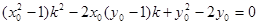 。
。
设两条切线PM,PN的斜率分别为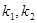 ,则
,则
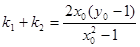 ,
,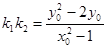 ,
9分
,
9分
且直线PM: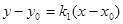 ,直线PN:
,直线PN: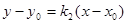 ,故
,故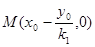 ,
,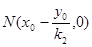
因此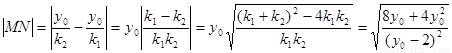 11分
11分
所以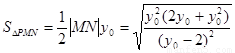 12分
12分
设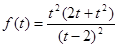 ,则
,则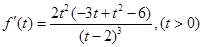
令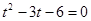 ,则
,则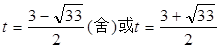 .
.
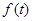 在
在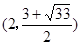 上单点递减,在
上单点递减,在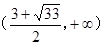 上单调递增,因此
上单调递增,因此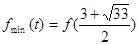
从而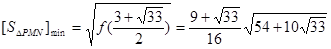 ,此时
,此时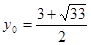 . 15分
. 15分
考点:1、抛物线的方程及性质;2、直线与圆的位置关系;3、直线与抛物线相交及与导数的综合应用

练习册系列答案
相关题目
 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 , 则有 ( )
, 则有 ( ) B.
B.
 D.
D.
 的焦点为
的焦点为 ,
, 过
过 轴的垂线交抛物线于
轴的垂线交抛物线于 两点.有下列四个命题:①
两点.有下列四个命题:① 必为直角三角形;②
必为直角三角形;② 必与抛物线相切;④直线
必与抛物线相切;④直线 的焦点为F,准线为
的焦点为F,准线为 ,经过F且斜率为
,经过F且斜率为 的直线与抛物线在
的直线与抛物线在 轴上方的部分相交于点A,且AK
轴上方的部分相交于点A,且AK
 的面积是( )
的面积是( ) C
C  D 8
D 8 的焦点为
的焦点为 ,点
,点 ,
, 在抛物线上,且
在抛物线上,且 ,则有( )
,则有( ) B.
B.
 D.
D.