��Ŀ����
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��ԲS������P����2 ![]() �������붨ԲQ����x��2
�������붨ԲQ����x��2 ![]() ��2+y2=36���У��Ƕ�ԲԲ��S�Ĺ켣Ϊ����C��
��2+y2=36���У��Ƕ�ԲԲ��S�Ĺ켣Ϊ����C��
��1��������C�ķ��̣�
��2��������C��x�ᣬy���������ֱ��ཻ��A��B���㣬��M��NΪ��ԲC����������㣬���е�M�ڵ�һ���ޣ���ֱ��AM��ֱ��BN��б�ʻ�Ϊ�෴�������ж�ֱ��MN��б���Ƿ�Ϊ��ֵ������Ƕ�ֵ��������ֵ��������Ƕ�ֵ��˵�����ɣ�
��3���ڣ�2�������£����ı���AMBN�����ȡֵ��Χ��
���𰸡�
��1���⣺��ԲS�İ뾶ΪR��
�ߵ� ![]() ��Բ
��Բ ![]() �ڣ�����Բ����
�ڣ�����Բ����
����PS=R��QS=6��R��
�� ![]() ��
��
��Բ��S�Ĺ켣Ϊ��P��QΪ���㣬���᳤Ϊ6����Բ
��2a=6��2c=4 ![]() ����a=3��c=2
����a=3��c=2 ![]() ����b2=1��
����b2=1��
������C�ķ���Ϊ ![]()
��2���⣺�ɣ�1����֪A��3��0����B��0��1��
��AM��б��Ϊk����ֱ��AM����Ϊy=k��x��3����ֱ��BN����Ϊy=��kx+1
�� ![]() ����M������Ϊ
����M������Ϊ ![]() ��
��
�� ![]() ����
���� ![]()
����MN��� 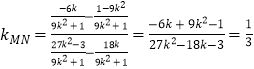
��3���⣺��MN�ķ���Ϊ ![]() ��
��
�� 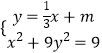 ����2x2+6mx+9m2��9=0
����2x2+6mx+9m2��9=0
�� ![]() ��
��
![]()
A��ֱ��MN�ľ���ֱ�Ϊ ![]()
B��ֱ��MN�ľ���ֱ�Ϊ ![]()
�����ı���AMBN��� ![]() =
= ![]()
�֩�1��m��1�������ı���AMBN�����ȡֵ��Χ�� ![]()
����������1��������Բ���пɵó�P S + Q S = P Q�������õ�Բ��S�Ĺ켣Ϊ��P��QΪ���㣬���᳤Ϊ6����Բ��������֪�����Բ�ķ��̡���2����б��ʽ�������ֱ�ߵķ��̣�������������Բ�ķ��̣����M��N��������꣬�������MN��б�ʡ���3������ֱ�ߺ���Բ�ķ��̣���ȥy�õ�����x�ķ���2x2+6mx+9m2��9=0������Τ�ﶨ������� x M+ x N ��xM .xN �ı���ʽ���ֱ����MN���Լ�A��ֱ��MN�ľ���ֱ�Ϊ d1 ��B��ֱ��MN�ľ���ֱ�Ϊ d2���������ı���AMBN��� S = S �� AMN + S �� BMN=![]() M N ( d 1 + d 2 ),�ٸ���m��ȡֵ��Χ�����õ�����AMBN�����ȡֵ��Χ��
M N ( d 1 + d 2 ),�ٸ���m��ȡֵ��Χ�����õ�����AMBN�����ȡֵ��Χ��

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�