题目内容
【题目】函数f(x)=|sinx|+|cosx|的最小正周期为m,函数g(x)=sin3x﹣sinx的最大值为n,则mn= .
【答案】![]()
【解析】解:∵函数f(x)=|sinx|+|cosx|= ![]() ,∴它的最小正周期为m=
,∴它的最小正周期为m= ![]() ,
,
∵令t=sinx∈[﹣1,1],函数g(x)=h(t)=t3﹣t,
求得 h′(t)=3t2﹣1=0,∴t=± ![]() ,
,
在区间(﹣ ![]() ,
, ![]() )上,h′(t)<0,故h(t)的减区间为(﹣
)上,h′(t)<0,故h(t)的减区间为(﹣ ![]() ,
, ![]() );
);
在区间(﹣1,﹣ ![]() )、(
)、( ![]() ,1)上,h′(t)>0,故h(t)的增区间为[﹣1,﹣
,1)上,h′(t)>0,故h(t)的增区间为[﹣1,﹣ ![]() )、(
)、( ![]() ,1];
,1];
故当t=﹣ ![]() 时,函数h(t)取得极大值为
时,函数h(t)取得极大值为 ![]() π,又h(1)=0,故h(t)的最大值为n=
π,又h(1)=0,故h(t)的最大值为n= ![]() ﹣(﹣
﹣(﹣ ![]() )=
)= ![]() ,
,
则mn= ![]() =
= ![]() .
.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】![]() 年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分
年年底,某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取若干市民对该项目进行评分(满分![]() 分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
分),绘制如下频率分布直方图,并将分数从低到高分为四个等级:
满意度评分 | 低于 60分 | 60分 到79分 | 80分 到89分 | 不低 于90分 |
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有![]() 人.
人.
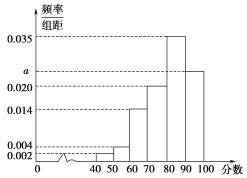
(1)求频率分布于直方图中![]() 的值,及评分等级不满意的人数;
的值,及评分等级不满意的人数;
(2)在等级为不满意市民中,老年人占![]() ,中青年占
,中青年占![]() ,现从该等级市民中按年龄分层抽取
,现从该等级市民中按年龄分层抽取![]() 人了解不满意的原因,并从中选取
人了解不满意的原因,并从中选取![]() 人担任整改督导员,求至少有一位老年督导员的概率;
人担任整改督导员,求至少有一位老年督导员的概率;
(3)相关部门对项目进行验收,验收的硬性指标是:市民对该项目的满意指数不低于![]() ,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.
,否则该项目需进行整改,根据你所学的统计知识,判断该项目能否通过验收,并说明理由.![]()
【题目】某人在连续7天的定点投篮的分数统计如下:在上述统计数据的分析中,一部分计算如右图所示的算法流程图(其中 ![]() 是这7个数据的平均数),则输出的S的值是( )
是这7个数据的平均数),则输出的S的值是( )
观测次数i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
观测数据ai | 5 | 6 | 8 | 6 | 8 | 8 | 8 |

A.1
B.![]()
C.![]()
D.![]()