题目内容
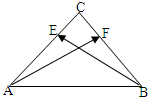 如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,|AE|=
如图直角三角形ABC中,|CA|=|CB|,|AB|=3,点E1,F分别在CA、CB上,EF∥AB,|AE|=| 2 |
| AF |
| BE |
分析:根据等腰Rt△ABC的斜边|AB|=3,算出|CA|=|CB|=
.由|AE|=
且EF∥AB,可得
=
且
=
,利用向量加法法则得到
=
+
且
=
+
.由此可得
•
=(
+
)•(
+
)=-
2+
•
-
•
+
•
,再根据向量的数量积公式分别算出
•
、
2、
•
与
•
的值,代入前面的式子算出
•
=-3,从而得到答案.
3
| ||
| 2 |
| 2 |
| AE |
| 2 |
| 3 |
| AC |
| BF |
| 2 |
| 3 |
| BC |
| AF |
| AB |
| 2 |
| 3 |
| BC |
| BE |
| BA |
| 2 |
| 3 |
| AC |
| AF |
| BE |
| AB |
| 2 |
| 3 |
| BC |
| BA |
| 2 |
| 3 |
| AC |
| AB |
| 2 |
| 3 |
| AB |
| AC |
| 2 |
| 3 |
| AB |
| BC |
| 4 |
| 9 |
| BC |
| AC |
| BC |
| AC |
| AB |
| AB |
| AC |
| AB |
| BC |
| AF |
| BE |
解答:解: ∵Rt△ABC中,|CA|=|CB|,|AB|=3,
∵Rt△ABC中,|CA|=|CB|,|AB|=3,
∴|CA|2+|CB|2=|AB|2=9,可得|CA|2=|CB|2=
,|CA|=|CB|=
.
而AC上的点E满足|AE|=
,可得|AE|=
|AC|.
又∵点E、F分别在CA、CB上,EF∥AB,
∴
=
=
,可得
=
,
由此可得
=
+
=
+
,同理可得
=
+
.
∴
•
=(
+
)•(
+
)=(
+
)•(-
+
)
=-
2+
•
-
•
+
•
∵
⊥
,∠CAB=∠CBA=45°,|CA|=|CB|=
,|AB|=3,
∴
•
=0,
2=
2=9,
•
=|
|•|
|cos45°=3×
×
=
,
•
=|
|•|
|cos135°=3×
×(-
)=-
.
因此,
•
=-
2+
•
-
•
+
•
=-9+
×
-
×(-
)+
×0=-3.
故答案为:-3
 ∵Rt△ABC中,|CA|=|CB|,|AB|=3,
∵Rt△ABC中,|CA|=|CB|,|AB|=3,∴|CA|2+|CB|2=|AB|2=9,可得|CA|2=|CB|2=
| 9 |
| 2 |
3
| ||
| 2 |
而AC上的点E满足|AE|=
| 2 |
| 2 |
| 3 |
又∵点E、F分别在CA、CB上,EF∥AB,
∴
| |AE| |
| |AC| |
| |BF| |
| |BC| |
| 2 |
| 3 |
| BF |
| 2 |
| 3 |
| BC |
由此可得
| AF |
| AB |
| BF |
| AB |
| 2 |
| 3 |
| BC |
| BE |
| BA |
| 2 |
| 3 |
| AC |
∴
| AF |
| BE |
| AB |
| 2 |
| 3 |
| BC |
| BA |
| 2 |
| 3 |
| AC |
| AB |
| 2 |
| 3 |
| BC |
| AB |
| 2 |
| 3 |
| AC |
=-
| AB |
| 2 |
| 3 |
| AB |
| AC |
| 2 |
| 3 |
| AB |
| BC |
| 4 |
| 9 |
| BC |
| AC |
∵
| BC |
| AC |
3
| ||
| 2 |
∴
| BC |
| AC |
| AB |
| |AB| |
| AB |
| AC |
| AB |
| AC |
3
| ||
| 2 |
| ||
| 2 |
| 9 |
| 2 |
| AB |
| BC |
| AB |
| BC |
3
| ||
| 2 |
| ||
| 2 |
| 9 |
| 2 |
因此,
| AF |
| BE |
| AB |
| 2 |
| 3 |
| AB |
| AC |
| 2 |
| 3 |
| AB |
| BC |
| 4 |
| 9 |
| BC |
| AC |
| 2 |
| 3 |
| 9 |
| 2 |
| 2 |
| 3 |
| 9 |
| 2 |
| 4 |
| 9 |
故答案为:-3
点评:本题在等腰直角三角形中求向量的数量积,着重考查了等腰直角三角形的性质、向量的线性运算性质、向量的数量积及其运算性质等知识,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
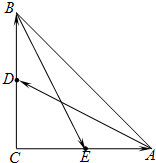 如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若
如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若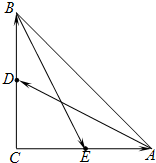 如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若
如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若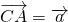 ,
,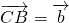 ,且
,且 =2.0
=2.0 、
、 表示
表示 和
和 ;
;