题目内容
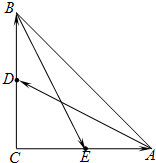 如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若
如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若| CA |
| a |
| CB |
| b |
| a |
| b |
(1)分别用向量
| a |
| b |
| AD |
| BE |
(2)计算AD、BE所成钝角的大小(结果用反三角函数表示).
分析:(1)利用向量的减法,即可用向量
、
表示
和
;
(2)由C=90°,可得
•
=0,设AD、BE所成的钝角为θ,利用向量的数量积,即可求得AD、BE所成钝角的大小.
| a |
| b |
| AD |
| BE |
(2)由C=90°,可得
| a |
| b |
解答:解:(1)
=
-
=
-
;(2分)
=
-
=
-
(2分)
(2)∵C=90°,∴
•
=0
设AD、BE所成的钝角为θ
∵|
|=
,|
|=
(2分)
∴cosθ=
=
=-
<0,
∴θ=π-arccos
.
所以AD、BE所成钝角的大小为π-arccos
(2分)
| AD |
| CD |
| CA |
| 1 |
| 2 |
| b |
| a |
| BE |
| CE |
| CB |
| 1 |
| 2 |
| a |
| b |
(2)∵C=90°,∴
| a |
| b |
设AD、BE所成的钝角为θ
∵|
| AD |
| 5 |
| BE |
| 5 |
∴cosθ=
| ||||
|
|
(
| ||||||||||||
|
|
| 4 |
| 5 |
∴θ=π-arccos
| 4 |
| 5 |
所以AD、BE所成钝角的大小为π-arccos
| 4 |
| 5 |
点评:本题考查向量的运算,考查向量的夹角,正确运用向量的数量积是关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
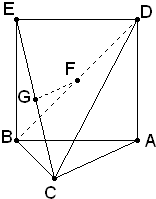 如图,三角形ABC中,AC=BC=
如图,三角形ABC中,AC=BC=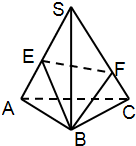 如图,S-ABC是正三棱锥且侧棱长为a,两侧棱SA,SC的夹角为30°,E,F分别是SA,SC上的动点,则三角形BEF的周长的最小值为( )
如图,S-ABC是正三棱锥且侧棱长为a,两侧棱SA,SC的夹角为30°,E,F分别是SA,SC上的动点,则三角形BEF的周长的最小值为( )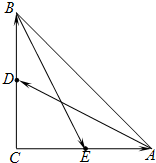 如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若
如图,三角形ABC是直角三角形,C=90°,边AC、BC的中点分别是E、D,若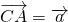 ,
,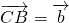 ,且
,且 =2.0
=2.0 、
、 表示
表示 和
和 ;
;