题目内容
设a、b是两条不同的直线,α、β是两个不重合的平面,则下列命题正确的是( )
分析:A、依照直线和平面平行的判定定理.条件之一是直线在平面外.
B、可举反例.
C、由两个平面互相垂直的判定定理,即可得到答案.
D、两个平面互相垂直的性质定理,应有n与α,β交线垂直.
B、可举反例.
C、由两个平面互相垂直的判定定理,即可得到答案.
D、两个平面互相垂直的性质定理,应有n与α,β交线垂直.
解答:解:A、若a∥α,a∥b,b?α,则b∥α,故A错误.
B、如图
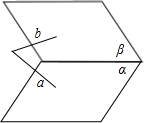
故B错误;
C、由于a∥β,则必存在b?β,有a∥b,
由于a⊥α,则b⊥α,故α⊥β,故C正确;
D、如图
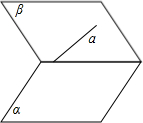
故断定D错误.
故选:C
B、如图

故B错误;
C、由于a∥β,则必存在b?β,有a∥b,
由于a⊥α,则b⊥α,故α⊥β,故C正确;
D、如图

故断定D错误.
故选:C
点评:直线和平面位置关系的判定定理和性质定理要注意前提条件.

练习册系列答案
相关题目