题目内容
设函数
 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )

 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )A. 在 在 单调递减 单调递减 | B. 在 在 单调递减 单调递减 |
C. 在 在 单调递增 单调递增 | D. 在 在 单调递增 单调递增 |
A
试题分析:
根据题意,由于函数

 的最小正周期为
的最小正周期为 ,故可知
,故可知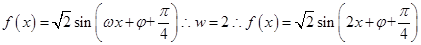 ,又因为
,又因为 ,则可知函数为偶函数,因此可知
,则可知函数为偶函数,因此可知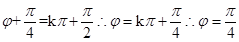 ,因此可知
,因此可知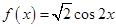 ,那么可知在
,那么可知在 单调递减,选A.
单调递减,选A.点评:解决该试题的关键是利用三角函数的周期公式和函数的偶函数性质得到参数的值,进而分析其单调区间,属于基础题。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目

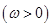 的图象向右平移
的图象向右平移 个单位长度后与函数
个单位长度后与函数 的图象重合,则
的图象重合,则 的最小值为( )
的最小值为( )

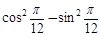 =( )
=( )

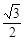

 的终边过点
的终边过点 ,则
,则 的值为( )
的值为( )


 (2)
(2) 
 ,给出下列四个说法:
,给出下列四个说法: ,则
,则 ;②
;②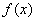 的最小正周期是
的最小正周期是 ;③
;③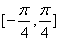 上是增函数; ④
上是增函数; ④ 对称. 其中正确说法的个数为( )
对称. 其中正确说法的个数为( )  为第二象限角,sin
为第二象限角,sin ,则cos
,则cos

 ,
, (0, π),则
(0, π),则 =
= 1
1

 的图象,只需将函数
的图象,只需将函数 的图象()
的图象() 个单位。
个单位。 倍,y值不变,再向左平移
倍,y值不变,再向左平移 单位。
单位。