Question

【题目】如图四边形ABCD为梯形，AD∥BC，∠ABC=90°，AD=2，AB=4，BC=5，图中阴影部分（梯形剪去一个扇形）绕AB旋转一周形成一个旋转体．
（1）求该旋转体的表面积；
（2）求该旋转体的体积．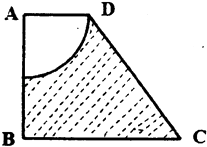

Answer 1

【答案】
（1）解：旋转后的几何体是一个圆台从上面挖去一个半球，圆台的上下底面半径分别

为2，5高为4，半球半径为2．

圆台的母线长为CD= =5．

∴ ，S圆台侧=π×（2+5）×5=35π， ，

∴旋转体的表面积为S表=8π+35π+25π=68π．

（2）解：V圆台= （4π+25π+10π）4=52π， ，

∴旋转体的体积为 ．

【解析】（1）旋转体为圆台挖去一个半球后的几何体，圆台的上下底面半径为AD，BC，高为AB，半球的半径为AD．于是几何体的表面积为圆台侧面积与底面积半球面积的和；（2）体积为圆台体积与半球体积的差．
【考点精析】本题主要考查了旋转体（圆柱、圆锥、圆台）的相关知识点，需要掌握常见的旋转体有：圆柱、圆锥、圆台、球才能正确解答此题．