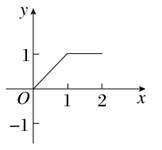
题目内容
设函数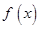 的定义域为D,如果
的定义域为D,如果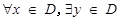 ,使得
,使得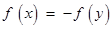
成立,则称函数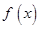 为“Ω函数”. 给出下列四个函数:①
为“Ω函数”. 给出下列四个函数:①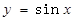 ;
;
②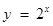 ;③
;③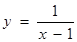 ;④
;④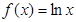 , 则其中“Ω函数”共有( )
, 则其中“Ω函数”共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
C
解析试题分析: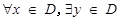 ,使得
,使得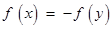 ,等价于
,等价于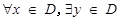 ,使得
,使得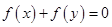 成立.
成立.
①因为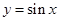 是奇函数,所以
是奇函数,所以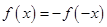 ,即当
,即当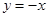 时,
时,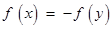 成立,故
成立,故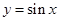 是“Ω函数”;
是“Ω函数”;
②因为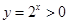 ,故
,故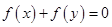 不成立,所以
不成立,所以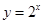 不是“Ω函数”;
不是“Ω函数”;
③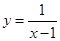 时,若
时,若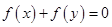 成立,则
成立,则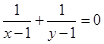 ,整理可得
,整理可得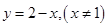 .即当
.即当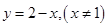 时,
时,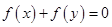 成立,故
成立,故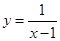 是“Ω函数”;
是“Ω函数”;
④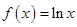 时,若
时,若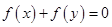 成立,则
成立,则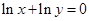 ,解得
,解得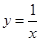 .即
.即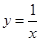 时,
时,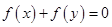 成立,故
成立,故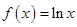 是“Ω函数”.
是“Ω函数”.
综上可得①③④中的函数均为“Ω函数”,所以C正确.
考点:新概念问题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
设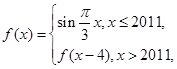 则f(2 016)=( )
则f(2 016)=( )
A.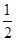 | B.-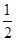 | C.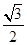 | D.-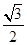 |
已知函数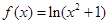 的值域为
的值域为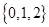 ,则满足这样条件的函数的个数有( )个.
,则满足这样条件的函数的个数有( )个.
| A.8 | B.9 | C.26 | D.27 |
已知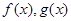 分别是定义在
分别是定义在 上的偶函数和奇函数,且
上的偶函数和奇函数,且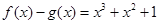 ,则
,则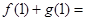
A.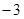 | B.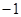 | C.1 | D.3 |
已知函数f(x)的定义域为[3,6],则函数y= 的定义域为( )
的定义域为( )
A.[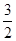 ,+∞) ,+∞) | B.[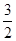 ,2) ,2) |
C.(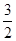 ,+∞) ,+∞) | D.[ ,2) ,2) |
若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=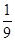 ,则f(x)的单调递减区间是( )
,则f(x)的单调递减区间是( )
| A.(-∞,2] | B.[2,+∞) |
| C.[-2,+∞) | D.(-∞,-2] |
若函数f(x)=x2-2x,g(x)=ax+2(a>0),?x1∈[-1,2],?x0∈[-1,2],使g(x1)=f(x0),则a的取值范围是( )
A.(0,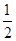 ] ] | B.[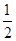 ,3] ,3] | C.[3,+∞) | D.(0,3] |
下列函数中,不满足f(2x)=2f(x)的是( )
| A.f(x)=|x| | B.f(x)=x-|x| |
| C.f(x)=x+1 | D.f(x)=-x |