题目内容
设集合A、B是非空集合,定义A×B={x|x∈A∪B且x?A∩B},已知A={x|y= },B={y|y=2x2},则A×B等于 ( )
},B={y|y=2x2},则A×B等于 ( )
A.(2,+∞) B.[0,1]∪[2,+∞)
C.[0,1)∪(2,+∞) D.[0,1]∪(2,+∞)
【答案】
A
【解析】
试题分析∵集合A、B是非空集合,定义A×B={x|x∈A∪B且x?A∩B},,A={x|y=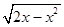 }={x|0
}={x|0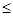 x
x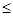 2},B={y|y=2x2}={y|y
2},B={y|y=2x2}={y|y 0},∴A∪B=[0,+∞),A∩B=[0,2],因此A×B=(2,+∞),,故选A.
0},∴A∪B=[0,+∞),A∩B=[0,2],因此A×B=(2,+∞),,故选A.
考点:集合交、并、补集的混合运算
点评:此题主要考查新定义、根式有意义的条件和集合交、并、补集的混合运算,新定义的题型是常见的题型,同学们要注意多练习这样的题

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目