题目内容
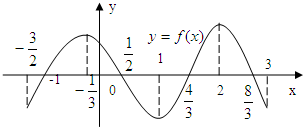 已知函数f(x)在定义域(-
已知函数f(x)在定义域(-| 3 |
| 2 |
分析:根据导数大于0时函数单调递增,导数小于0时原函数单调递减确定不等式f′(x)≤0的解集可得答案.
解答:解:由y=f(x)图象可知f(x)在[-
,1],[2,3)递减.
如图,
∵根据导数大于0时函数单调递增,导数小于0时原函数单调递减,
∴不等式f′(x)≤0⇒x∈[-
,1]∪[2,3).
故选A.
| 1 |
| 3 |
如图,
∵根据导数大于0时函数单调递增,导数小于0时原函数单调递减,
∴不等式f′(x)≤0⇒x∈[-
| 1 |
| 3 |
故选A.
点评:本题主要考查了导数的正负和原函数增减性的问题,导数的符号决定函数的单调性:导数为正,函数单增;导数为负,函数递减.属基础题.

练习册系列答案
相关题目
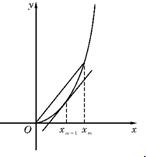 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.