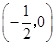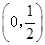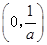题目内容
已知函数f(x)=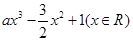 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间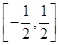 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
【答案】
(Ⅰ)y=6x-9. (Ⅱ)0<a<5.
【解析】(I)当a=1时,利用导数求出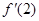 的值,也就是切线的斜率,进而可写出点斜式方程,再化成一般式方程即可.
的值,也就是切线的斜率,进而可写出点斜式方程,再化成一般式方程即可.
(II)本小题的实质是求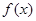 在
在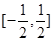 上最小值,满足
上最小值,满足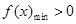 即可.
即可.
由于涉及到参数a,所以再求最小值时需要对a值进行讨论
(Ⅰ)当a=1时,f(x)=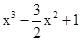 ,f(2)=3;f’(x)=
,f(2)=3;f’(x)=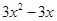 ,
f’(2)=6.所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9.
,
f’(2)=6.所以曲线y=f(x)在点(2,f(2))处的切线方程为y-3=6(x-2),即y=6x-9.
(Ⅱ)f’(x)=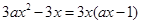 .令f’(x)=0,解得x=0或x=
.令f’(x)=0,解得x=0或x=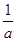 .
.
以下分两种情况讨论:
(1)
若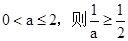 ,当x变化时,f’(x),f(x) 的变化情况如下表:
,当x变化时,f’(x),f(x) 的变化情况如下表:
|
X |
|
0 |
|
|
f’(x) |
+ |
0 |
- |
|
f(x) |
|
极大值 |
|
当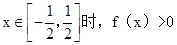 等价于
等价于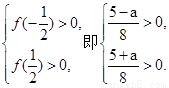
解不等式组得 -5<a<5. 因此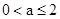 .
.
(2)
若a>2,则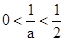 .当x变化时,f’(x), f(x)的变化情况如下表:
.当x变化时,f’(x), f(x)的变化情况如下表:
|
X |
|
0 |
|
|
|
|
f’(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
|
极小值 |
|
当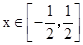 时,f(x)>0等价于
时,f(x)>0等价于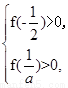 即
即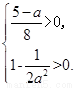
解不等式组得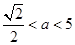 或
或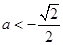 .因此2<a<5.
.因此2<a<5.
综合(1)和(2),可知a的取值范围为0<a<5.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|