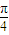题目内容
已知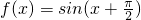 ,g(x)=sinx,下列选项正确的是
,g(x)=sinx,下列选项正确的是
- A.函数y=f(x)g(x)的一个单调区间是[-
 ,
, ]
] - B.函数y=f(x)+g(x)的最大值是2
- C.函数y=f(x)+g(x)的一个对称中心是(-
 ,0)
,0) - D.函数f(x)的一条对称轴是x=

C
分析:利用三角函数的恒等变换化简 y=f(x)g(x)和y=f(x)+g(x)的解析式,利用三角函数的对称性、最值、单调性等得到答案.
解答:①∵f(x)=sin(x+ )=cosx,其对称轴为 x+
)=cosx,其对称轴为 x+ =kπ,k∈z,故排除D.
=kπ,k∈z,故排除D.
②∵由于函数f(x)g(x)=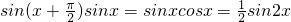 ,由 2kπ-
,由 2kπ- ≤2x≤2kπ+
≤2x≤2kπ+ ,k∈z,可得其增区间为[kπ-
,k∈z,可得其增区间为[kπ- ,kπ+
,kπ+ ];
];
由 2kπ+ ≤2x≤2kπ+
≤2x≤2kπ+ ,可得其减区间为[kπ+
,可得其减区间为[kπ+ ,kπ+
,kπ+ ],k∈z,故排除A.
],k∈z,故排除A.
③由于函数f(x)+g(x)=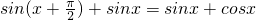 =
= ,其最大值为
,其最大值为 ,故排除B.
,故排除B.
再由x+ =kπ,可得 x=kπ-
=kπ,可得 x=kπ- ,故其对称中心为(kπ-
,故其对称中心为(kπ- ,0),故C正确.
,0),故C正确.
故选C.
点评:本小题考查诱导公式、三角函数的对称性、最值、单调性等,属于基础题.
分析:利用三角函数的恒等变换化简 y=f(x)g(x)和y=f(x)+g(x)的解析式,利用三角函数的对称性、最值、单调性等得到答案.
解答:①∵f(x)=sin(x+
 )=cosx,其对称轴为 x+
)=cosx,其对称轴为 x+ =kπ,k∈z,故排除D.
=kπ,k∈z,故排除D.②∵由于函数f(x)g(x)=
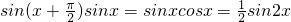 ,由 2kπ-
,由 2kπ- ≤2x≤2kπ+
≤2x≤2kπ+ ,k∈z,可得其增区间为[kπ-
,k∈z,可得其增区间为[kπ- ,kπ+
,kπ+ ];
];由 2kπ+
 ≤2x≤2kπ+
≤2x≤2kπ+ ,可得其减区间为[kπ+
,可得其减区间为[kπ+ ,kπ+
,kπ+ ],k∈z,故排除A.
],k∈z,故排除A.③由于函数f(x)+g(x)=
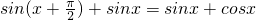 =
= ,其最大值为
,其最大值为 ,故排除B.
,故排除B.再由x+
 =kπ,可得 x=kπ-
=kπ,可得 x=kπ- ,故其对称中心为(kπ-
,故其对称中心为(kπ- ,0),故C正确.
,0),故C正确.故选C.
点评:本小题考查诱导公式、三角函数的对称性、最值、单调性等,属于基础题.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
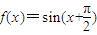 ,g(x)=sinx,下列选项正确的是( )
,g(x)=sinx,下列选项正确的是( )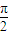 ,
,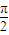 ]
]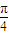 ,0)
,0)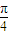
 sinx-cosx,且f(x)=
sinx-cosx,且f(x)= g′(x)(g(x)+cosx)
g′(x)(g(x)+cosx) 时,f(x)函数的值域;
时,f(x)函数的值域; ,求角C.
,求角C.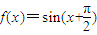 ,g(x)=sinx,下列选项正确的是( )
,g(x)=sinx,下列选项正确的是( )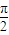 ,
,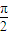 ]
] ,0)
,0)