题目内容
在
中，
则AB+3BC的最大值为 .
解析试题分析：∵B=60°，A+B+C=180°，∴A+C=120°，由正弦定理得
，∴AB=2sinC，BC=2sinA．∴AB+3BC=2sinC+6sinA=2sin（120°-A）+6sinA=2（sin120°cosA-cos120°sinA）+6sinA=
cosA+7sinA=sin（A+φ），（其中tanφ=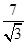
），所以AB+3BC的最大值为．
考点：本题考查了正弦定理及三角函数的有界性
点评：解题时要认真审题，注意正弦定理和三角函数恒等变换的合理运用
练习册系列答案
激活思维优加课堂系列答案
活力试卷系列答案
相关题目
中，内角
所对边分别是
，已知
,
，则
中,
,边
上的中线
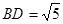,则
．
，则角A的大小为 
，则角A等于 .
，C=60°，c=1，则最短边的边长是 .
中，角
所对的边分别为
，若
，
，则角
的值为 ．
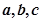，若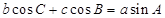
，则△ABC是 三角形
，点D 在BC边上，∠ADC=45°，则AD的长度等于______.