Question

对自行车运动员甲、乙两人在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下：试判断选谁参加该项重大比赛更合适．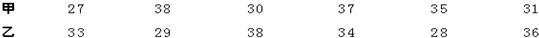

Answer 1

分析：先做出甲和乙的速度的平均数，甲和乙的速度的平均数相同，需要再比较两组数据的方差，选方差较小运动员参加比赛比较好．

解答：解：平均速度

.

x

甲=

1

6

（27+38+30+37+35+31）=33；

.

x

乙=

1

6

（33+29+38+34+28+36）=33．
s_甲²=

1

6

[（-6）²+5²+（-3）²+4²+2²+（-2）²]=

47

3

；
s_乙²=

1

6

[（-4）²+5²+1²+（-5）²+3²]=

37

3

．
∵

.

x

甲=

.

x

乙，s_甲²＞s_乙²，
∴乙的成绩比甲稳定．
应选乙参加比赛更合适．

点评：本题考查两组数据的平均数和方差，对于两组数据，通常要求的是这组数据的方差和平均数，用这两个特征数来表示分别表示两组数据的特征．