题目内容
已知函数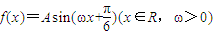 的最小正周期为T=6π,且f(2π)=2.
的最小正周期为T=6π,且f(2π)=2.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设α,β∈[0,
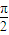 ],
],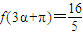 ,
,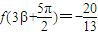 ,求cos(α-β)的值.
,求cos(α-β)的值.
【答案】分析:(Ⅰ)由函数的最值求出A,由周期求出ω,从而求得函数的解析式.
(Ⅱ)由 f(3α+π)=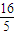 ,利用诱导公式求得cosα的值,可得sinα的值.由
,利用诱导公式求得cosα的值,可得sinα的值.由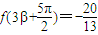 求得sinβ,可得cosβ,再利用两角和差的余弦公式求得cos(α-β)=cosαcosβ+sinαsinβ的值.
求得sinβ,可得cosβ,再利用两角和差的余弦公式求得cos(α-β)=cosαcosβ+sinαsinβ的值.
解答:解:(Ⅰ)依题意得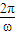 =6π,ω=
=6π,ω= .…(2分)
.…(2分)
∴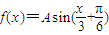 .再由f(2π)=2得
.再由f(2π)=2得 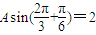 ,即 Asin
,即 Asin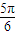 =2,
=2,
∴A=4,…(4分)
∴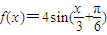 …(6分)
…(6分)
(Ⅱ)由 f(3α+π)=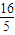 得
得 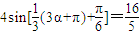 ,即
,即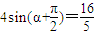
∴cosα=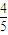 ,又∵α∈[0,
,又∵α∈[0,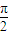 ],∴sinα=
],∴sinα=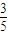 .. …(8分)
.. …(8分)
由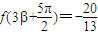 得
得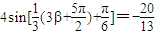 ,即 sin(β+π)=-
,即 sin(β+π)=-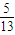 ,
,
∴sinβ=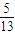 ,又∵β∈[0
,又∵β∈[0 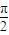 ],∴cosβ=
],∴cosβ=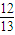 . …(10分)
. …(10分)
从而cos(α-β)=cosαcosβ+sinαsinβ=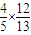 +
+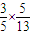 =
=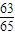 . …(12分)
. …(12分)
点评:本题主要考查两角和差的正弦、余弦公式的应用,同角三角函数的基本关系,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.
(Ⅱ)由 f(3α+π)=
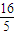 ,利用诱导公式求得cosα的值,可得sinα的值.由
,利用诱导公式求得cosα的值,可得sinα的值.由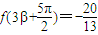 求得sinβ,可得cosβ,再利用两角和差的余弦公式求得cos(α-β)=cosαcosβ+sinαsinβ的值.
求得sinβ,可得cosβ,再利用两角和差的余弦公式求得cos(α-β)=cosαcosβ+sinαsinβ的值.解答:解:(Ⅰ)依题意得
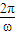 =6π,ω=
=6π,ω= .…(2分)
.…(2分)∴
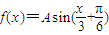 .再由f(2π)=2得
.再由f(2π)=2得 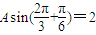 ,即 Asin
,即 Asin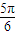 =2,
=2,∴A=4,…(4分)
∴
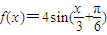 …(6分)
…(6分)(Ⅱ)由 f(3α+π)=
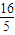 得
得 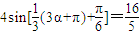 ,即
,即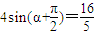
∴cosα=
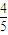 ,又∵α∈[0,
,又∵α∈[0,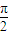 ],∴sinα=
],∴sinα=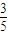 .. …(8分)
.. …(8分)由
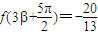 得
得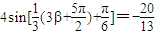 ,即 sin(β+π)=-
,即 sin(β+π)=-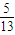 ,
,∴sinβ=
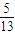 ,又∵β∈[0
,又∵β∈[0 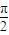 ],∴cosβ=
],∴cosβ=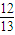 . …(10分)
. …(10分)从而cos(α-β)=cosαcosβ+sinαsinβ=
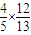 +
+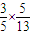 =
=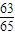 . …(12分)
. …(12分)点评:本题主要考查两角和差的正弦、余弦公式的应用,同角三角函数的基本关系,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 的最小正周期为
的最小正周期为 ,将其图象向左平移
,将其图象向左平移 个单位长度,所得图象关于
个单位长度,所得图象关于 轴对称,则
轴对称,则 的一个可能值是
( )
的一个可能值是
( ) B.
B. C.
C. D.
D.
 的最小正周期为2π.
的最小正周期为2π. ,求
,求 的值.
的值. 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围. 的最小正周期为
的最小正周期为 .
. 的值;
的值; 的最小正周期为
的最小正周期为
 的值;
的值;
 在
在
 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.