题目内容
(本题满分12)
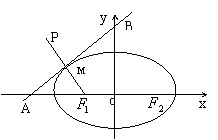
如图,已知椭圆C: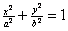 (a>b>0)的左、右焦点分别是
(a>b>0)的左、右焦点分别是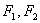 ,离心率为e.直线L:y=ex+a与x轴、y轴分别交于A、B点,M是直线L与椭圆C的一个公共点,P是点
,离心率为e.直线L:y=ex+a与x轴、y轴分别交于A、B点,M是直线L与椭圆C的一个公共点,P是点 关于直线L的对称点。设
关于直线L的对称点。设 。
。
(Ⅰ)证明: =1-
=1- ;
(Ⅱ)确定
;
(Ⅱ)确定 的值,使得△P
的值,使得△P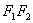 是等腰三角形。
是等腰三角形。
 |
【答案】
解:
(Ⅰ) 因为A,B分别是直线l:y=ex+a与x轴,y轴的交点,所以A,B的坐标分别是(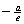 ,0),(0,a).
,0),(0,a).
由{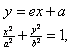 得 {
得 {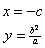 这里 c=
这里 c=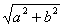 ,所以点M的坐标是(-c,
,所以点M的坐标是(-c,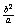 ).
).
由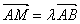 得(-c+
得(-c+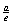 ,
,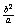 )=
)=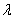 (
(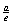 ,a),即{
,a),即{ ,解得
,解得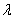 =1-
=1-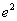
………………………………6分
(Ⅱ)因为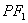 ⊥l,所以∠P
⊥l,所以∠P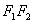 =90°+∠
=90°+∠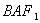 ,为钝角。要使△P
,为钝角。要使△P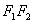 是等腰三角形,必有
是等腰三角形,必有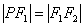 ,即
,即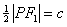 .
.
设点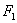 到l的距离为d,由
到l的距离为d,由 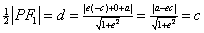 ,
,
得
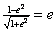 ,
,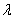 =1-
=1-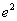 =
=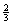 ,所以
,所以 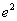 =
=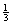 ,于是
,于是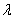 =1-
=1-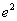 =
=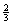 .
.
即当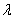 =
=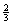 时,△P
时,△P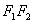 是等腰三角形。 ………………………………12分
是等腰三角形。 ………………………………12分

练习册系列答案
相关题目
 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
 ⊥矩形
⊥矩形 所在的平面,
所在的平面, 分别是
分别是 、
、 的中点,
的中点,
 ∥平面
∥平面 ;
; ;
; ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
. M、N分别是
M、N分别是 CD.
CD. ,求直线AC与平面BCD所成的角.
,求直线AC与平面BCD所成的角.
 的底面
的底面 是正方形,侧面
是正方形,侧面 是等腰三角形且垂直于底面,
是等腰三角形且垂直于底面, ,
, ,
, 、
、 分别是
分别是 、
、 的中点。
的中点。 ;
; 的大小。
的大小。