题目内容
4.设m>1,x,y满足约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$,且目标函数z=x+my的最大值为2,则m的取值为( )| A. | 2 | B. | 1+$\sqrt{2}$ | C. | 3 | D. | 2+$\sqrt{2}$ |
分析 根据m>1,可以判断直线y=mx的倾斜角位于区间($\frac{π}{4},\frac{π}{2}$)上,由此判断出满足约束条件件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$的平面区域的形状,再根据目标函数z=x+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此可得关于m的方程,从而求得m值.
解答  解:∵m>1,由约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$作出可行域如图,
解:∵m>1,由约束条件$\left\{\begin{array}{l}{y≥x}\\{y≤mx}\\{x+y≤1}\end{array}\right.$作出可行域如图,
直线y=mx与直线x+y=1交于($\frac{1}{m+1},\frac{m}{m+1}$),
目标函数z=x+my对应的直线与直线y=mx垂直,且在($\frac{1}{m+1},\frac{m}{m+1}$)处取得最大值,
由题意可知$\frac{1+{m}^{2}}{m+1}=2$,
又∵m>1,解得m=1+$\sqrt{2}$.
故选:B.
点评 本题考查的知识点是简单线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
9.设全集为R,集合A={x||x|<3},B={x|-1<x≤5},则A∩(∁RB)=( )
| A. | (-3,0) | B. | (-3,-1] | C. | (-3,-1) | D. | (-3,3) |
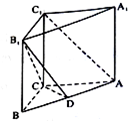 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.