题目内容

已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），且P在线段AB上，
AP
=t
AB
（0≤t≤1）则
OA
•
OP
的最大值为
 
．
分析：先利用响亮的三角形法则将
OP
用
OA
和
OB
表达，再由数量积的坐标运算得到关于t的式子求最值即可．
解答：解：
OA
•
OP
=
OA
•(
OA
+
AP
)=
OA
•(
OA
+
tAB
)=
OA
•(
OA
+t(
OB
-
OA
))=
OA
•((1-t)
OA
-t
0B
)=(1-t)
OA
-2t
OA
•
OB
=（1-t）9
因为0≤t≤1，所以（1-t）9≤9，最大值为9，所以
OA
•
OP
的最大值为9
故答案为：9
点评：本题考查向量的表示、数量积运算等知识，属基本运算运算的考查．
练习册系列答案
相关题目
已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），点P在线段AB上，且
AP
=t
AB
(0≤t≤1)，则
OA
•
OP
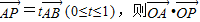的最大值为（　　）
已知O、A、B三点的坐标分别为O(0,0)、A(3,0)、B(0,3)，点P在线段AB上，且=t(0≤t≤1),则·的最大值为(    )

A.3                  B.6                   C.9                     D.12

已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），点P在线段AB上，且
AP
=t
AB
(0≤t≤1)，则
OA
•
OP
的最大值为（　　）
A．3B．6C．9D．12
已知O、A、B三点的坐标分别为O（0，0），A（3，0），B（0，3），点P在线段AB上，且的最大值为（ ）
A．3
B．6
C．9
D．12

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网