题目内容
已知p:-2≤x≤3; q:-m≤x≤1+m,(m>0),若p是q的充分不必要条件,求实数m的取值范围.
【答案】分析:通过p是q的充分不必要条件,列出关系式,即可求解m的范围.
解答:解:因为p:-2≤x≤3; q:-m≤x≤1+m,(m>0),p是q的充分不必要条件,
所以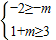 ,所以m≥2.当m=2时,p是q的充要条件,又m>0
,所以m≥2.当m=2时,p是q的充要条件,又m>0
所以实数m的取值范围:(2,+∞).
点评:本题考查充要条件的应用,注意两个命题的端点值不能同时成立,这是易错点.
解答:解:因为p:-2≤x≤3; q:-m≤x≤1+m,(m>0),p是q的充分不必要条件,
所以
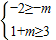 ,所以m≥2.当m=2时,p是q的充要条件,又m>0
,所以m≥2.当m=2时,p是q的充要条件,又m>0所以实数m的取值范围:(2,+∞).
点评:本题考查充要条件的应用,注意两个命题的端点值不能同时成立,这是易错点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目