题目内容
函数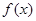 的定义域为
的定义域为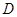 ,若存在非零实数
,若存在非零实数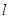 使得对于任意
使得对于任意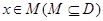 ,有
,有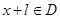 ,且
,且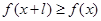 ,则称
,则称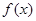 为
为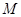 上的
上的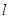 高调函数。如果定义域为
高调函数。如果定义域为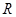 的函数
的函数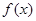 是奇函数,当
是奇函数,当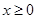 时,
时,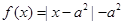 ,且
,且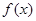 为
为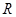 上的4高调函数,那么实数
上的4高调函数,那么实数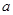 的取值范围是( )
的取值范围是( )
A.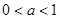 B.
B. 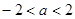 C.
C. D.
D.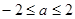
【答案】
C
【解析】解:定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x-a2|-a2= x-2a2 (x≥a2) -x (0≤x<a2) ,的图象如图,∵f(x)为R上的4高调函数,当x<0时,函数的最大值为a2,要满足f(x+l)≥f(x),4大于等于区间长度3a2-(-a2),∴4≥3a2-(-a2),∴-1≤a≤1,故选C

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目