题目内容
设集合M="{x|" x>2},P={x|x<3},那么“x∈M∪P”是“x∈M∩P”的( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分也不必要条件 |
A
分析:根据所给的两个集合,写出两个集合的交集和并集,根据两个集合中的元素,看出两个元素之间的包含关系,得到结果.
解答:解:∵集合M={x|x>2},N={x|x<3},
∵x∈{x|x∈M或x∈N}表示x∈M∪N=R,
M∩N={x|2<x<3}
∴x∈M∪N=R不一定推出x∈M∩N,
x∈M∩N?x∈M∪N=R,
故“x∈M∪P”是“x∈M∩P”的必要不充分条件,
故选A.
解答:解:∵集合M={x|x>2},N={x|x<3},
∵x∈{x|x∈M或x∈N}表示x∈M∪N=R,
M∩N={x|2<x<3}
∴x∈M∪N=R不一定推出x∈M∩N,
x∈M∩N?x∈M∪N=R,
故“x∈M∪P”是“x∈M∩P”的必要不充分条件,
故选A.

练习册系列答案
相关题目
 ,则“
,则“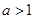 ”是“
”是“ ”的( )
”的( )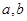 是实数,则“
是实数,则“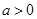 且
且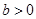 ”是“
”是“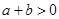 且
且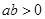 ”的
”的  、
、 是
是 的两个内角,若
的两个内角,若 ,
, ,则
,则 是
是 的( )
的( )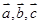 为非零的平面向量,甲:
为非零的平面向量,甲: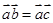 ,乙:
,乙: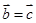 ,则甲是乙的( )
,则甲是乙的( ) ”是“函数
”是“函数 为偶函数”的 ( )
为偶函数”的 ( )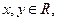 那么
那么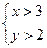 是
是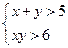 成立的 ( )
成立的 ( ) 必要不充分条件
必要不充分条件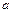 、
、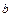 为两条不同的直线,
为两条不同的直线,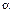 、
、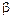 为两个不同的平面,则
为两个不同的平面,则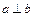 的一个充分条件是( )
的一个充分条件是( )


