题目内容
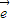 1、
1、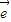 2是不共线的向量,
2是不共线的向量,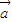 =
=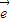 1+k
1+k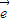 2,
2,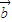 =k
=k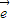 1+
1+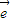 2,则
2,则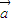 与
与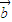 共线的充要条件是实数k等于( )
共线的充要条件是实数k等于( )A.0
B.-1
C.-2
D.±1
【答案】分析:本题考查的知识是平面向量的基本定理,平面向量的充要条件,由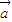 与
与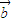 共线?存在实数m,使
共线?存在实数m,使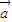 =m
=m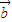 ,然后根据平面向量的基本定理,我们可以构造一个关于m,k的方程,解方程即可得到结论.
,然后根据平面向量的基本定理,我们可以构造一个关于m,k的方程,解方程即可得到结论.
解答:解: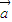 与
与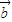 共线?存在实数m,使
共线?存在实数m,使 =m
=m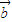 ,
,
即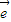 1+k
1+k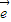 2=mk
2=mk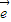 1+m
1+m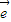 2.又
2.又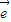 1、
1、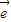 2不共线,
2不共线,
∴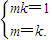
∴k=±1.
故选D
点评: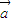 与
与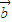 共线?存在实数m,使
共线?存在实数m,使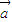 =m
=m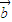 ,这是判断两个向量(可能是平面向量,也可能是空间向量)最常用的方法.
,这是判断两个向量(可能是平面向量,也可能是空间向量)最常用的方法.
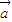 与
与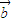 共线?存在实数m,使
共线?存在实数m,使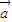 =m
=m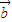 ,然后根据平面向量的基本定理,我们可以构造一个关于m,k的方程,解方程即可得到结论.
,然后根据平面向量的基本定理,我们可以构造一个关于m,k的方程,解方程即可得到结论.解答:解:
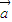 与
与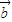 共线?存在实数m,使
共线?存在实数m,使 =m
=m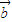 ,
,即
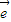 1+k
1+k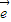 2=mk
2=mk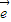 1+m
1+m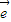 2.又
2.又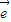 1、
1、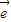 2不共线,
2不共线,∴
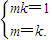
∴k=±1.
故选D
点评:
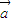 与
与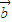 共线?存在实数m,使
共线?存在实数m,使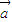 =m
=m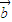 ,这是判断两个向量(可能是平面向量,也可能是空间向量)最常用的方法.
,这是判断两个向量(可能是平面向量,也可能是空间向量)最常用的方法. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知
,
是不共线的向量,若
=λ1
+
,
=
+λ2
(λ1,λ2∈R),则A、B、C三点共线的充要条件为( )
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
| A、λ1=λ2=-1 |
| B、λ1=λ2=1 |
| C、λ1λ2-1=0 |
| D、λ1•λ2+1=1 |
 1、
1、 =
= =k
=k