题目内容
已知:如下图,P是正方形ABCD所在平面外一点,PA=PB=PC=PD=a,AB=a.
求:平面APB与平面CPD相交所成较大的二面角的余弦值.

答案:
解析:
解析:
|
解:因为AB∥CD,CD 所以AB∥平面CPD. 又P∈平面APB,且P∈平面CPD, 因此平面APB∩平面CPD=l,且P∈l. 所以二面角B-l-C就是平面APB和平面CPD相交所得到的一个二面角. 因为AB∥平面CPD,AB 所以AB∥l. 过P作PE⊥AB,PE⊥CD. 因为l∥AB∥CD, 因此PE⊥l,PF⊥l, 所以∠EPF是二面角B-l-C的平面角. 因为PE是正三角形APB的一条高线,且AB=a, 因为E,F分别是AB,CD的中点, 所以EF=BC=a. 在△EFP中, 分析:为了找到二面角及其平面角,必须依据题目的条件,找出两个平面的交线. |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
(本小题满分12分)
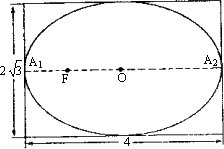
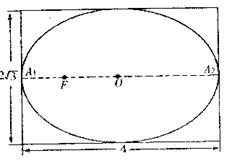
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
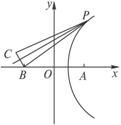
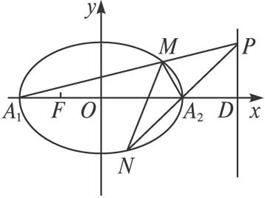
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.